
【题目】平面直角坐标系中,点P的坐标为(m,n),则向量![]() 可以用点P的坐标表示为
可以用点P的坐标表示为![]() =(m,n);已知
=(m,n);已知![]() =(x1,y1),
=(x1,y1),![]() =(x2,y2),若x1x2+y1y2=0,则
=(x2,y2),若x1x2+y1y2=0,则![]() 与
与![]() 互相垂直.
互相垂直.
下面四组向量:①![]() =(3,﹣9),
=(3,﹣9),![]() =(1,﹣
=(1,﹣![]() );
);
②![]() =(2,π0),
=(2,π0),![]() =(2﹣1,﹣1);
=(2﹣1,﹣1);
③![]() =(cos30°,tan45°),
=(cos30°,tan45°),![]() =(sin30°,tan45°);
=(sin30°,tan45°);
④![]() =(
=(![]() +2,
+2,![]() ),
),![]() =(
=(![]() ﹣2,
﹣2,![]() ).
).
其中互相垂直的组有( )
A. 1组 B. 2组 C. 3组 D. 4组
科目:初中数学 来源: 题型:
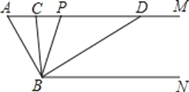
【题目】如图,已知AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,直接写出∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②
中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②![]() ;③
;③![]() .
.
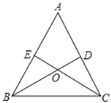
(1)上述三个条件中,由哪两个条件可以判定![]() 是等腰三角形?(用序号写出所有成立的情形)
是等腰三角形?(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形,说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
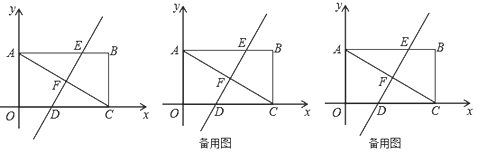
【题目】如图,平面直角坐标系中,矩形![]() 的对角线
的对角线![]() ,
,![]() .
.
(1)把矩形![]() 沿直线
沿直线![]() 对折,使点
对折,使点![]() 落在点
落在点![]() 处,折痕
处,折痕![]() 分别与
分别与![]() 、
、![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() 、
、![]() ,求直线
,求直线![]() 的解析式;
的解析式;
(2)若点![]() 在直线
在直线![]() 上,平面内是否存在点
上,平面内是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,请直接写出点
为顶点的四边形是菱形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)整式![]() 表示
表示![]() 、
、![]() 两数和的平方
两数和的平方
整式![]() 表示
表示![]() 、
、![]() 两数差的平方
两数差的平方
仿照上例填空:整式![]() 表示:______.
表示:______.
整式![]() 表示:______.
表示:______.
(2)试计算![]() 、
、![]() 取不同数值时,
取不同数值时,![]() 及
及![]() 的值填入下表:
的值填入下表:
| 当 | 当 | 当 | 当 |
| ||||
|
(3)根据上表,我发现的规律______.
(4)用发现的规律计算:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F是平行四边形ABCD对角线AC上两点,AE=CF=![]() AC.连接DE,DF并延长,分别交AB,BC于点G,H,连接GH,则
AC.连接DE,DF并延长,分别交AB,BC于点G,H,连接GH,则![]() 的值为( )
的值为( )
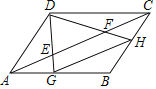
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某购物网店在双十一期间实行打折促销活动,规定如下表:
次性购物不大于100元不打折,不大于300元但大于100元打九折,超过300元的部分打八折.
(1)王老师一次性购物600元,他实际付款多少元?
(2)若顾客在该网店一次性购物![]() 元,当
元,当![]() 低于300元但大于100元时,他实际付款多少元?当
低于300元但大于100元时,他实际付款多少元?当![]() 大于300元时,他实际付款多少元?(用含
大于300元时,他实际付款多少元?(用含![]() 的式子表示)
的式子表示)
(3)如果王老师两次购物货款合计820元,第一次购物的货款为![]() 元
元![]() ,用含
,用含![]() 的式子表示两次购物王老师实际付款多少元?
的式子表示两次购物王老师实际付款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月,我市某中学举行了“爱我中国朗诵比赛”活动,根据学生的成绩划分为A、B、C、D四个等级,并绘制了不完整的两种统计图.根据图中提供的信息,回答下列问题:
(1)参加朗诵比赛的学生共有 人,并把条形统计图补充完整;
(2)扇形统计图中,m= ,n= ;C等级对应扇形有圆心角为 度;
(3)学校欲从获A等级的学生中随机选取2人,参加市举办的朗诵比赛,请利用列表法或树形图法,求获A等级的小明参加市朗诵比赛的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
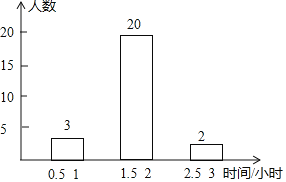
【题目】某校七年级开展了为期一周的“敬老爱亲”社会活动,并根据学生做家务的时间来评价他们在活动中的表现,学校随机抽查了部分学生在这次活动中做家务的时间,并绘制了如下的频数分布表和频数分布直方图.请根据图表中提供的信息,解答下列问题:
等级 | 做家务时间(小时) | 频数 | 百分比 |
A | 0.5≤x<1 | 3 | 6% |
B | 1<x<1.5 | a | 30% |
C | 1.5≤x<2 | 20 | 40% |
D | 2≤x<2.5 | b | m |
E | 2.5≤x<3 | 2 | 4% |
(1)这次活动中抽查的学生有______人,表中a=______,b=______,m=______,并补全频数分布直方图;
(2)若该校七年级有700名学生,请估计这所学校七年级学生一周做家务时间不足2小时而又不低于1小时的大约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com