
如图所示,△ABC中,BC=4,∠B=![]() ,AB=3
,AB=3![]() ,M、N分别为AB、AC上的点,MN∥BC,并设MN=x,△MNC的面积为S.
,M、N分别为AB、AC上的点,MN∥BC,并设MN=x,△MNC的面积为S.
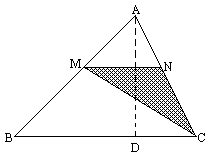
(1)求出S与x之间的函数关系式,并写出自变量x的取值范围;
(2)是否存在平行线段MN,使△MNC的面积等于2.若存在,求出MN的长;若不存在,请说明理由.
|
解:(1)过A点作AD⊥BC,垂足为D,则有AD= 设△MNC的边MN上的高为h. ∵MN∥BC.∴ ∴h= ∴S= =- (2)若存在这样的平行线段MN,使S△MNC=2,则方程- |
|
第(1)小题求S与x的函数关系式,只需把x看作一个确定的值,在题设以及MN=x的条件下,求△MNC的面积,得到的结果是一个含x的表达式,把x看作变量,这个表达式就是S与x的函数关系式.一般地说,在求函数关系式时,可以把自变量x看作一个确定的值,由此求出因变量y的值,得到的表达式就是y与x的函数关系式. 自变量x的取值范围是使函数关系有意义的自变量的值的全体,本题中要在题设条件下构成△MNC,x的取值范围只能是0与4之间的一切实数. 第(2)小题相当于问:是否存在x使S=2,这就成了一个十分简单的关于二次方程求解的问题. 本题不难,但涉及函数概念以及几何、代数、三角中的多个知识点,是一道较好的综合题. |


 天天练口算系列答案
天天练口算系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com