
【题目】如图,![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上的中点,点
边上的中点,点![]() 是
是![]() 边上的一个动点,延长
边上的一个动点,延长![]() 到
到![]() ,使
,使![]() ,作
,作![]() ,其中
,其中![]() 点在
点在![]() 上.
上.
(1)如图①,若![]() ,则
,则![]() _______.
_______.
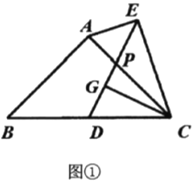
(2)如图②,若![]() ,求
,求![]() 的值;
的值;
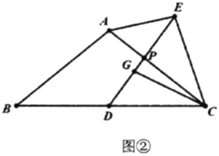
(3)如图③,若![]() ,延长
,延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() ,在点
,在点![]() 运动的过程中,探究:当
运动的过程中,探究:当![]() 的值为多少时,线段
的值为多少时,线段![]() 与
与![]() 的长度和取得最小值?
的长度和取得最小值?
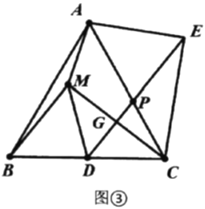
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3)![]()
【解析】
(1)连接AD,首先证明AC=![]() CD,再证明△DCG∽△ACE,可得
CD,再证明△DCG∽△ACE,可得![]() ;
;
(2)连接AD.证明△DCG∽△ACE,可得![]() ,设AB=AC=5k,BD=CD=4k,则AD=
,设AB=AC=5k,BD=CD=4k,则AD=![]() ,由此即可解决问题;
,由此即可解决问题;
(3)由题意,当A,M,D共线时,AM+DM的值最小.想办法证明∠GDM=∠GDC=45°,设CH=![]() ,则PC=2
,则PC=2![]() ,PH=DH=
,PH=DH=![]() ,推出AC=2CD=2(
,推出AC=2CD=2(![]() ),由此即可解决问题.
),由此即可解决问题.
(1)如图,连接AD,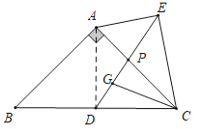
∵AB=AC,∠B=45°,
∴△ABC是等腰直角三角形,
∵BD=CD,
∴AD⊥BC,
∴AD=BD=DC,
∴AC=![]() CD,
CD,
∵∠CDE=∠CAE,∠DCG=∠ACE,
∴△DCG∽△ACE,
∴![]() ;
;
(2)如图,连接AD,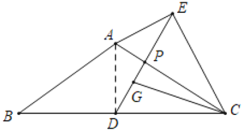
∵∠CDE=∠CAE,∠DCG=∠ACE,
∴△DCG∽△ACE,
∴![]() ,
,
∵AB=AC,BD=CD,
∴AD⊥BC,
设AB=AC=5k,BD=CD=4k,
则AD=![]() ,
,
∴![]() ;
;
(3)如图,由题意知,当A、M、D三点共线时,AM+DM的值最小.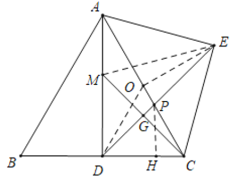
连EM,取AC的中点O,连接OE,OD,作PH⊥CD于H.
∵AB=AC,∠B=60°,
∴△ABC是等边三角形,
∴BC=AC,∠ACB=60°,
∵BD=CD,
∴AD⊥BC,
∴∠CDA=90°,
∴AC=2CD,
∵∠CDE=∠CAE,∠DCG=∠ACE,
∴△DCG∽△ACE,
∴![]() ,
,
∴EC=2CG,
∵CM=2CG,
∴CM=CE,∠DCG=∠ACE,
∵∠ACD=∠DCG+∠GCP=∠ACE+∠GCP=∠ECM=60°,
∴△ECM是等边三角形,
∵CD=CO,∠DCM=∠OCE,CM=CE,
∴△DCM≌△OCE(SAS),
∴OE=DM,
∵∠CDE=∠CAE,
∴A,D,C,E四点共圆,
∴∠ADC+∠AEC=180°,
∴∠AEC=90°,
∵OA=OC,
∴OE=OC=CD=DM,
∵CG=GM,
∴∠GDM=∠GDC=45°,
设CH=![]() ,则PC=
,则PC=![]() ,PH=DH=
,PH=DH=![]() ,
,
∴AC=2CD=2(![]() ),
),
∴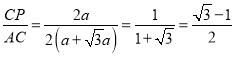 .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC>AB>AC,D是边BC上的一个动点(点D不与点B、C重合),将△ABC沿AD折叠,点B落在点B'处,连接BB',B'C,若△BCB'是等腰三角形,则符合条件的点D的个数是
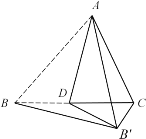
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
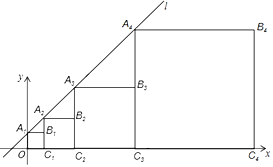
【题目】在平面直角坐标系中,直线l:y=x+1与y轴交于点A1,如图所示,依次作正方形OA1B1C1,正方形C1A2B2C2,正方形C2A3B3C3,正方形C3A4B4C4,……,点A1,A2,A3,A4,……在直线l上,点C1,C2,C3,C4,……在x轴正半轴上,则前n个正方形对角线长的和是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
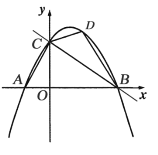
【题目】如图,在平面直角坐标系中,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴相交于点B、C,经过点B、C的抛物线
轴相交于点B、C,经过点B、C的抛物线![]() 与
与![]() 轴的另一个交点为A.
轴的另一个交点为A.
(1)求出抛物线表达式,并求出点A坐标;
(2)已知点D在抛物线上,且横坐标为3,求出△BCD的面积;
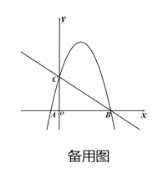
(3)点P是直线BC上方的抛物线上一动点,过点P作PQ垂直于![]() 轴,垂足为Q.是否存在点P,使得以点A、P、Q为顶点的三角形与△BOC相似?若存在,请求出点P的坐标;若不存在,请说明理由.
轴,垂足为Q.是否存在点P,使得以点A、P、Q为顶点的三角形与△BOC相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据《国家学生体质健康标准》规定:九年级男生坐位体前屈达到17.8厘米及以上为优秀;达到13.8厘米至17.7厘米为良好;达到![]() 厘米至13.7厘米为及格;达到
厘米至13.7厘米为及格;达到![]() 厘米及以下为不及格.某校为了了解九年级男生的身体柔韧性情况,从该校九年级男生中随机抽取了20%的学生进行坐位体前屈测试,并把测试结果绘制成如图所示的统计表和扇形统计图(部分信息不完整),请根据所给信息解答下列问题.
厘米及以下为不及格.某校为了了解九年级男生的身体柔韧性情况,从该校九年级男生中随机抽取了20%的学生进行坐位体前屈测试,并把测试结果绘制成如图所示的统计表和扇形统计图(部分信息不完整),请根据所给信息解答下列问题.
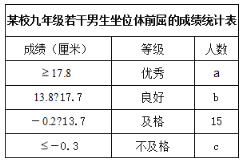
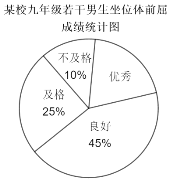
(1)求参加本次坐位体前屈测试人数;
(2)求a、b、c的值;
(3)试估计该年级男生中坐位体前屈成绩不低于13.8厘米的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
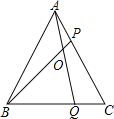
【题目】如图,在等边三角形ABC的AC,BC边上各取一点P,Q,使AP=CQ,AQ,BP相交于点O.若BO=6,PO=2,则AP的长,AO的长分别为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将每件进价为80元的A商品按每件100元出售,一天可售出128件.经过市场调查,发现这种商品的销售单价每降低1元,其日销量可增加8件.设该商品每件降价x元,商场一天可通过A商品获利润y元.
(1)求y与x之间的函数解析式(不必写出自变量x的取值范围)
(2)A商品销售单价为多少时,该商场每天通过A商品所获的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了解旅游人数的变化情况,收集并整理了2017年1月至2019年12月期间的月接待旅游量(单位:万人次)的数据并绘制了统计图如下:
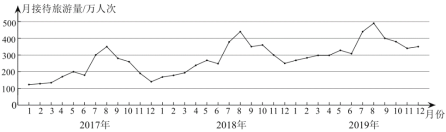
根据统计图提供的信息,下列推断不合理的是( )
A.2017年至2019年,各年的月接待旅游量高峰期大致在7,8月份
B.2019年的月接待旅游量的平均值超过300万人次
C.2017年至2019年,年接待旅游量逐年增加
D.2017年至2019年,各年下半年(7月至12月)的月接待旅游量相对于上半年(1月至6月)波动性更小,变化比较平稳
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com