
����Ŀ��ij����Ͷ������һ�ֻ������ܳɱ�Ϊ2000��Ԫ�����û���������������Ϊ10̨����������70̨ʱ��ÿ̨�ɱ�y����������x֮����һ�κ�����ϵ������y���Ա���x�IJ��ֶ�Ӧֵ���±���
![]()
��1����y��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2����û���������������
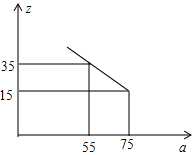
��3���г����鷢�֣����ֻ���ÿ��������z��̨�����ۼ�a����Ԫ�M̨��֮��������ͼ��ʾ�ĺ�����ϵ���ó��������ֻ������һ���°�ͬһ�ۼ۹��������ֻ���40̨����������ó���һ�����������ֻ���������ע������=�ۼ�-�ɱ���
���𰸡���1�� y=-![]() x+65��10��x��70����2�� 50̨����3�� 312.5��Ԫ.
x+65��10��x��70����2�� 50̨����3�� 312.5��Ԫ.
��������
�����������1����y��x֮��Ĺ�ϵʽΪy=kx+b�����ô���ϵ�����Ϳ���������ϵʽ���ɸû���������������Ϊ10̨����������70̨�Ϳ���ȷ���Ա�����ȡֵ��Χ��
��2������ÿ̨�ijɱ������������������ܳɱ��������������⼴�ɣ�
��3����ÿ��������z��̨�����ۼ�a����Ԫ�M̨��֮��ĺ�����ϵʽΪz=ma+n�����ô���ϵ������������ʽ���ٽ�z=25�������ʽ���a��ֵ���Ϳ������ÿ̨�����Ӷ����������
�����������1����y��x֮��Ĺ�ϵʽΪy=kx+b�������⣬��
![]() ��
��
��ã�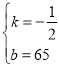 ��
��
��y=-![]() x+65��
x+65��
���û���������������Ϊ10̨����������70̨��
��10��x��70��
��2�������⣬��
xy=2000��
-![]() x2+65x=2000��
x2+65x=2000��
-x2+130x-4000=0��
��ã�x1=50��x2=80��70����ȥ����
�𣺸û�������������Ϊ50̨��
��3����ÿ��������z��̨�����ۼ�a����Ԫ�M̨��֮��ĺ�����ϵʽΪz=ma+n���ɺ���ͼ��
![]() ��
��
��ã�![]() ��
��
��z=-a+90��
��z=25ʱ��a=65��
�ɱ�y=-![]() z+65=-
z+65=-![]() ��25+65=
��25+65=![]() ����Ԫ����
����Ԫ����
��������25��65-![]() ��=
��=![]() =312.5����Ԫ����
=312.5����Ԫ����
�𣺸ó���һ�����������ֻ���������Ϊ312.5��Ԫ��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ������ABC�У�AQ=PQ��PR=PS��PR��AB��R��PS��AC��S�����������ۣ���AS=AR����QP��AR���ۡ�BPR�ա�QPS�У� ��
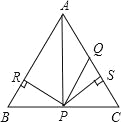
A��ȫ����ȷ B������������ȷ C��������ȷ D������������ȷ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������2xy=16x3y2�������Ӧ��ĵ���ʽ�ǣ� ��
A. 4x2y B. 8x3y2 C. 4x2y2 D. 8x2y
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O��ֱ��ABΪ10cm����BCΪ5cm��D��E�ֱ�����ACB��ƽ��������O��AB�Ľ��㣬PΪAB�ӳ�����һ�㣬��PC=PE��

��1����AC��AD�ij���
��2�����ж�ֱ��PC����O��λ�ù�ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x�IJ���ʽ3-x��a�Ľ⼯Ϊx��4�������m�IJ���ʽ2m+3a��1�Ľ�Ϊ��������
A. m��2 B. m��1 C. m��-2 D. m��-1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ʒ�Ľ���Ϊ800Ԫ�����Ϊ1200Ԫ�����ڸ���Ʒ��ѹ���̵����������ۣ���Ҫ��֤�����ʲ�����20%������Ϳɴ� ��
A. 8�� B. 8.5�� C. 7�� D. 6��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���y=k x+b�����㣨��3����4���ͣ�0��2����
��1����k��b��ֵ��
��2����һ�κ���ͼ����x�ᡢy��ֱ��ڵ�A��B����A��B�����꣮
��3����P�Ǹú����ϵ�һ�㣬��P�ĺ�����Ϊ![]() ����PO�ij���
����PO�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������P(2��a��3a��6)����������ľ�����ȣ����P��������( )
A. (3��3) B. (3����3)��(6����6) C. (6����6) D. (3��3)��(6����6)
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com