
【题目】甲、乙两人同时开始采摘樱桃,甲平均每小时采摘8公斤樱桃,乙平均每小时采摘7公斤樱桃。采摘同时结束后,甲从他采摘的樱桃中取出1公斤给了乙,这时两人的樱桃一样多。他们采摘樱桃用了多长时间?设他们采摘了x小时,则下面所列方程中正确的是( )
A. 8x-1=7x+1 B. 8x-1=7x C. 8x+l=7x D. 8x+l=7x-1
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
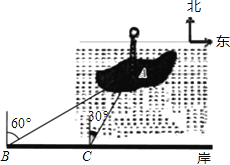
【题目】如图,郴州北湖公园的小岛上有为了纪念唐代著名诗人韩愈而建的韩愈铜像,其底部为A,某人在岸边的B处测得A在B的北偏东60°的方向上,然后沿岸边直行200米到达C处,再次测得A在C的北偏东30°的方向上(其中A,B,C在同一平面上).求这个铜像底部A到岸边BC的距离(结果精确到0.1米,参考数据:![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,BE⊥AC于E,且D、E分别是AB、AC的中点.延长BC至点F,使CF=CE.

(1)求∠ABC的度数;
(2)求证:BE=FE;
(3)若AB=2,求△CEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣x+m=0有两个不相等的实数根.
(1)求实数m的取值范围;
(2)若方程的两个实数根为x1、x2,且x1+x2+x1x2=m2﹣1,求实数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα=![]() =
=![]() ,根据上述角的余切定义,解下列问题:
,根据上述角的余切定义,解下列问题:
(1)如图1,若BC=3,AB=5,则ctanB= ;
(2)ctan60°= ;
(3)如图2,已知:△ABC中,∠B是锐角,ctan C=2,AB=10,BC=20,试求∠B的余弦cosB的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时点C与点A恰好在同一水平线上,点A、B、P、C在同一平面内.
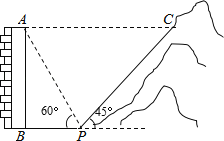
(1)若BP=10m,求居民楼AB的高度;(精确到0.1,![]() ≈1.732)
≈1.732)
(2)若PC=24m,求C、A之间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com