
����Ŀ�����κ���y=ax2+bx+4��ͼ����x�ύ������A��B����y�ύ�ڵ�C����A����1��0����B��4��0��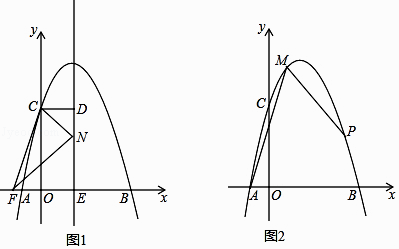
��1����˶��κ����ı���ʽ
��2����ͼ1�������ߵĶԳ���m��x�ύ�ڵ�E��CD��m������ΪD����F���� ![]() ��0��������N���߶�DE���˶�������CF��CN��FN�����Ե�C��D��NΪ��������������FEN���ƣ����N������
��0��������N���߶�DE���˶�������CF��CN��FN�����Ե�C��D��NΪ��������������FEN���ƣ����N������
��3����ͼ2����M���������ϣ��ҵ�M�ĺ�������1����PΪ��������һ���㣬����PMA=45�㣬���P�����꣮
���𰸡�
��1��
�⣺��x=0ʱ��y=4��
��C��0��4����
�������ߵĽ���ʽΪy=a��x+1����x��4��������C���������ã���4a=4�����a=��1��
�������ߵĽ���ʽΪy=��x2+3x+4
��2��
�⣺x=�� ![]() =
= ![]() ��
��
��CD= ![]() ��EF=
��EF= ![]() ��
��
���N�������� ![]() ��a����ND=4��a��NE=a��
��a����ND=4��a��NE=a��
����CDN�ס�FENʱ�� ![]() ����
���� ![]() �����a=
�����a= ![]() ��
��
���N�������� ![]() ��
�� ![]() ����
����
����CDN�ס�NEFʱ�� ![]() ����
���� ![]() =
= ![]() ����ã�a=2��
����ã�a=2��
���N�������� ![]() ��2����
��2����
������������N�������� ![]() ��
�� ![]() ����
���� ![]() ��2��
��2��
��3��
�⣺��ͼ��ʾ������A��AD��y�ᣬ����M��DM��x�ᣬ����ΪD������A��AE��AM��ȡAE=AM����EF��x�ᣬ����ΪF������EM�����������P��

��AM=AE����MAE=90�㣬
���AMP=45�㣮
��x=1���������ߵĽ���ʽ�ã�y=6��
���M��������1��6����
��MD=2��AD=6��
�ߡ�DAM+��MAF=90�㣬��MAF+��FAE=90�㣬
���DAM=��FAE��
�ڡ�ADM�͡�AFE�У�  ��
��
���ADM�ա�AFE��
��EF=DM=2��AF=AD=6��
��E��5����2����
��EM�Ľ���ʽΪy=kx+b��
����M�͵�E���������ã� ![]() �����k=��2��b=8��
�����k=��2��b=8��
��ֱ��EM�Ľ���ʽΪy=��2x+8��
��y=��2x+8��y=��x2+3x+4��������ã�x=1��x=4��
��x=4����y=��2x+8�ã�y=0��
���P��������4��0��
����������1������õ�C�����꣬�������ߵĽ���ʽΪy=a��x+1����x��4��������C������������a��ֵ���Ӷ��õ������ߵĽ���ʽ����2������������ߵĶԳ��ᣬȻ�����CD��EF�ij������N������Ϊ��0��a����ND=4��a��NE=a��Ȼ���������������ε������г�����a�ķ��̣�Ȼ������a��ֵ����3������A��AD��y�ᣬ����M��DM��x�ᣬ����ΪD������A��AE��AM��ȡAE=AM����EF��x�ᣬ����ΪF������EM�����������P�����AMEΪ����ֱ�������Σ�Ȼ������õ�M�����꣬�Ӷ��ɵõ�MD=2��AD=6��Ȼ��֤�����ADM�ա�AFE�����ǿɵõ���E�����꣬Ȼ�����EM�Ľ���ʽΪy=��2x+8��������ֱ��EM�������ߵĽ������꼴�ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC������֪��D���߶�AB�ķ����ӳ���������AC���е�F���߶�GE����DAC��ƽ������E����BC��G����AE��BC��
��1����֤����ABC�ǵ�����������
��2����AE��8��AB��10��GC��2BG������ABC���ܳ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���x2����m��2��x����2m��1��=0��
��1����֤�����̺�����������ȵ�ʵ������
��2�����˷��̵�һ������1����������̵���һ�����������Դ�����Ϊ�߳���ֱ�������ε��ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У�ACƽ����DAB����ADC����ACB��90�㣬EΪAB���е㣬����CE������DE��AC��F��AD��4��AB��6.
(1)��֤����ADC�ס�ACB��
(2)��AC��ֵ��
(3)��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������6�֣���֪��ֽ������һ���ᣨ��ͼ��ʾ����
![]()
����һ��
��1���۵�ֽ�棬ʹ��1��ʾ�ĵ�������1��ʾ�ĵ��غϣ����ʱ����2��ʾ�ĵ����� ��ʾ�ĵ��غϣ�
��������
��2���۵�ֽ�棬ʹ��5��ʾ�ĵ�������1��ʾ�ĵ��غϣ��ش��������⣺
����6��ʾ�ĵ����� ��ʾ�ĵ��غϣ�
���������۵�����������A��B����Ҳ�غϣ���A��B����֮��ľ���Ϊ11��A��B����ࣩ����A���ʾ����Ϊ ��B���ʾ����Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���������³�����������ڼ�ٰ�ѧ��ר�����ֻᣬ�볡ȯ��Ϊ����Ʊ������Ʊ����������Ʊռ������![]() ������ǰ��Ʊ������費ͬ������Żݣ��������·��ڣ�����Ʊÿ��12Ԫ�����۳�����Ʊ����
������ǰ��Ʊ������費ͬ������Żݣ��������·��ڣ�����Ʊÿ��12Ԫ�����۳�����Ʊ����![]() ������Ʊÿ��16Ԫ�����۳�����Ʊ����һ�룻��������·��ڣ�����Ʊ��ÿ��16Ԫ���ۣ����ƻ������·��۳�ȫ����Ʊ�������·�����Ʊ��ÿ��xԪ���ۣ���Ʊ��Ϊa�ţ�
������Ʊÿ��16Ԫ�����۳�����Ʊ����һ�룻��������·��ڣ�����Ʊ��ÿ��16Ԫ���ۣ����ƻ������·��۳�ȫ����Ʊ�������·�����Ʊ��ÿ��xԪ���ۣ���Ʊ��Ϊa�ţ�
(1)���·ݵ�Ʊ��������Ϊ_____Ԫ�����·ݵ�������Ϊ______Ԫ��
(2)��xΪ����ʱ������ʹ�������µ�Ʊ�������ƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���BAC��90����AB��AC����DΪBC���е㣬ֱ�ǡ�MDN�Ƶ�D��ת��DM��DN�ֱ����AB��AC����E��F���㣬���н��ۣ��١�DEF�ǵ���ֱ�������Σ���AE��CF���ۡ�BDE�ա�ADF����BE��CF��EF��������ȷ�������� ��

A. �٢ڢ� B. �ڢۢ�
C. �٢ڢ� D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����꣬��ʡ�����ˡ������۾�������������ʽ��ijСѧΪ���˽���꼶�����Ӿ����������һ�����꼶���ӵ�ѧ��������ͳ�ƣ��õ�ÿ����͵Ľ��ӵĶ�ͯ�����ֱ�Ϊ20��30��20��34��36��40�������������ݣ�����˵��������ǣ� ��
A.ƽ������30
B.������20
C.�����34
D.������ ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ������У�����������ִ������������в����ݳ����ɼ�����ѡ��![]() ��ѡ����ɳ��д����Ӻ��д����Ӳμ�ѧУ������ÿ����
��ѡ����ɳ��д����Ӻ��д����Ӳμ�ѧУ������ÿ����![]() ��ѡ�ֵľ����ɼ���ͼ��ʾ��
��ѡ�ֵľ����ɼ���ͼ��ʾ��

![]() �����
�����
ƽ�������֣� | ��λ�����֣� | �������֣� | |
������� |
|
| |
������� |
|
|
![]() ������Ӿ����ɼ���ƽ��������λ���������ĸ������ӵijɼ��Ϻã�
������Ӿ����ɼ���ƽ��������λ���������ĸ������ӵijɼ��Ϻã�
![]() �������Ӿ����ɼ��ķ�����ж��ĸ������ӵijɼ���Ϊ�ȶ���
�������Ӿ����ɼ��ķ�����ж��ĸ������ӵijɼ���Ϊ�ȶ���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com