
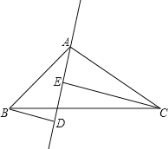
【题目】已知△ABC中,AB=AC,∠BAC=120°,在BC上取一点O,以O为圆心、OB为半径作圆,且⊙O过A点. 如图①,若⊙O的半径为5,求线段OC的长;
如图②,过点A作AD∥BC交⊙O于点D,连接BD,求 ![]() 的值.
的值.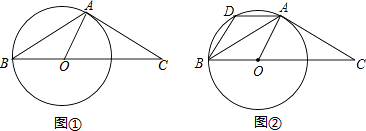
【答案】解:∵△ABC中,AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵OA=OB,
∴∠BAO=∠B=30°,
∴∠AOC=30°+30°=60°,
∴∠OAC=90°,
∵OA=5,
∴OC=2AO=10.
连接OD,
∵∠AOC=60°,AD∥BC,
∴∠DAO=∠AOC=60°,
∵OD=OA,
∴∠ADO=60°,
∴∠DOB=∠ADO=60°,
∵OD=OB,
∴△DOB是等边三角形,
∴BD=OB=OA,
在Rt△OAC中,OC=2BD,由勾股定理得:AC= ![]() BD,
BD,
∴ ![]() =
= ![]() .
.

【解析】求出∠B=∠C=30°,求出∠AOC=60°,求出∠OAC=90°,得出OC=2OA即可.根据勾股定理求出AC,求出△BOD是等边三角形,求出AC= ![]() BD,即可求出答案.
BD,即可求出答案.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )

A. BE=DF B. BF=DE C. AE=CF D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小明和爸爸在800米的环形跑道上骑车锻炼,他们在同一地点沿着同一方向同时出发,骑行结束后两人有如下对话:
小明:您要5分钟才能第一次追上我.
爸爸:我骑完一圈的时候,你才骑了半圈!
(1)请根据他们的对话内容,求小明和爸爸的骑行速度(速度单位:米/分钟);
(2)爸爸第一次追上小明后,在第二次相遇前,再经过多少分钟,小明和爸爸相距80米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD中,AB=3,BC=4,E,F两点分别在边AB,BC上运动,△BEF沿EF折叠后为△GEF,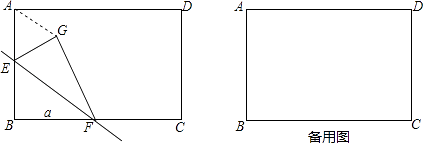
(1)若BF=a,则线段AG的最小值为 . (用含a的代数式表示)
(2)问:在E、F运动过程中,取a= 时,AG有最小值,值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ADC=900,∠BAD=600,对角线AC平分∠BAD,且AB=AC=4,点E、F分别是AC、BC的中点,连接DE,EF,DF,则DF的长为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正值重庆一中85年校庆之际,学校计划利用校友慈善基金购买一些平板电脑和打印机.经市场调查,已知购买1台平板电脑比购买3台打印机多花费600元,购买2台平板电脑和3台打印机共需8400元.
(1)求购买1台平板电脑和1台打印机各需多少元?
(2)学校根据实际情况,决定购买平板电脑和打印机共100台,要求购买的总费用不超过168000元,且购买打印机的台数不低于购买平板电脑台数的2倍.请问最多能购买平板电脑多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
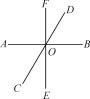
【题目】如图,直线AB,CD,EF相交于点O.
(1)写出∠COE的邻补角;
(2)分别写出∠COE和∠BOE的对顶角;
(3)如果∠BOD=60°,∠BOF=90°,求∠AOF和∠FOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为12,在其角上去掉两个全等的矩形DMNP和矩形BIJK,DM=IB=2,DP=BK=3,正方形EFGH顶点分别在正方形ABCD的边上,且EH过N点,则正方形EFGH的边长是( )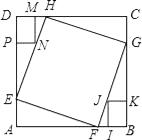
A.10
B.3 ![]()
C.4 ![]()
D.3 ![]() 或4
或4 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是过点
是过点![]() 的直线,
的直线,![]() 于
于![]() ,
,![]() 于点
于点![]() ;
;
(1)若![]() 、
、![]() 在
在![]() 的同侧(如图所示)且
的同侧(如图所示)且![]() .求证:
.求证:![]() ;
;

(2)若![]() 、
、![]() 在
在![]() 的两侧(如图所示),且
的两侧(如图所示),且![]() ,其他条件不变,
,其他条件不变,![]() 与
与![]() 仍垂直吗?若是请给出证明;若不是,请说明理由.
仍垂直吗?若是请给出证明;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com