
【题目】一个装有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,接着关闭进水管直到容器内的水放完,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.
(1)当4≤x≤12时,求y与x的函数解析式;
(2)每分进水、出水各多少升?
(3)第 分钟时该容器内的水恰好为10升.

科目:初中数学 来源: 题型:
【题目】完成下面的证明,如图点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DE∥BA,DF∥CA.求证:∠FDE=∠A.
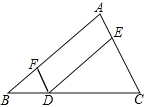
证明:∵DE∥AB,
∴∠FDE=∠ ( )
∵DF∥CA,
∴∠A=∠ ( )
∴∠FDE=∠A( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=ax+b和反比例函数y= ![]() 在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象可能是( )
在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象可能是( ) 
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为﹣1和3,则下列结论正确的是( ) 
A.2a﹣b=0
B.a+b+c>0
C.3a﹣c=0
D.当a= ![]() 时,△ABD是等腰直角三角形
时,△ABD是等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=(2m-3)x+m+2.
(1)若函数图像过原点,求m的值;
(2)若函数图像过点(-1,0),求m的值;
(3)若函数图像平行于直线y=-x+2求m的值;
(4)若函数图像经过第一、二、四象限,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CA=CB,M,N分别AB上的两动点,且∠MCN=45°,下列结论:①![]() ;②CM2﹣CN2=NBNA﹣MBMA;③AM2+BN2=MN2;④S△CAM+S△CBN=S△CMN,其中正确的有( )
;②CM2﹣CN2=NBNA﹣MBMA;③AM2+BN2=MN2;④S△CAM+S△CBN=S△CMN,其中正确的有( )
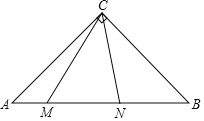
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,数轴上标出若干个点,每相邻两点相距一个单位长度,点A,B,C,D对应的数分别是数a,b,c,d,且d-2a=10,那么数轴的原点应是( )![]()
A.点A
B.点B
C.点C
D.点D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC的角平分线BD,CE相交于点P.
(1)如果∠A=80,求∠BPC= .
(2)如图②,过点P作直线MN∥BC,分别交AB和AC于点M和N,试求∠MPB+∠NPC的度数(用含∠A的代数式表示) .
(3)将直线MN绕点P旋转。
(i)当直线MN与AB,AC的交点仍分别在线段AB和AC上时,如图③,试探索∠MPB,∠NPC,∠A三者之间的数量关系,并说明你的理由。
(ii)当直线MN与AB的交点仍在线段AB上,而与AC的交点在AC的延长线上时,如图④,试问(i)中∠MPB,∠NPC,∠A三者之间的数量关系是否仍然成立?若成立,请说明你的理由;若不成立,请给出∠MPB,∠NPC,∠A三者之间的数量关系,并说明你的理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com