
【题目】已知△ABC在平面直角坐标系中的位置如图所示:
(1)画出△ABC绕点A按逆时针方向旋转90°后的△A′B′C′;
(2)在(1)的条件下,求点C旋转到点C′所经过的路线长及线段AC旋转到新位置时所划过区域的面积.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某公司生产一种新型生物医药产品,生产成本为2万元/ 吨,每月生产能力为12吨,且生产出的产品都能销售出去.这种产品部分内销,另一部分外销(出口),内销与外销的单价![]() (单位:万元/吨)与销量的关系分别如图1,图2.
(单位:万元/吨)与销量的关系分别如图1,图2.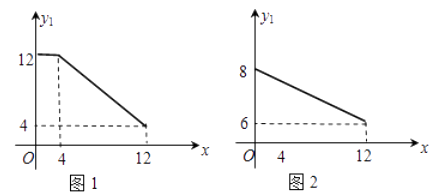
(1)如果该公司内销数量为x(单位:吨),内、外销单价分别为y 1 , y 2 ,求, ![]() 关于x的函数解析式;
关于x的函数解析式;
(2)如果该公司内销数量为x(单位:吨),求内销获得的毛利润 ![]() 关于x的函数解析式;
关于x的函数解析式;
(3)请设计一种销售方案,使该公司本月能获得最大毛利润,并求出毛利润的最大值.(毛利润=销售收入-生产成本).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形纸片![]() 中,
中,![]() 点
点![]() 为
为![]() 上一点,将
上一点,将![]() 沿
沿![]() 折叠,刚好使点
折叠,刚好使点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处.
处.

![]() 用尺规作图,在图上作出折叠线
用尺规作图,在图上作出折叠线![]() .以及点
.以及点![]() 的对称点
的对称点![]() (不写作法,但要保留作图痕迹,)
(不写作法,但要保留作图痕迹,)
![]() 求
求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的口袋里装有白、黄、蓝三种颜色的乒乓球(除颜色外其余都相同),其中白球有2个,黄球有1个,再从中任意摸出1个球是白球的概率为 ![]() .
.
(1)试求袋中蓝球的个数;
(2)第一次任意摸出一个球(不放回),第二次再摸出一个球,请用树状图或列表法表示两次摸到球的所有可能结果,并求两次摸到的球都是白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,三角形ABC的位置如图所示,把三角形ABC平移后,三角形ABC内任意点P(x,y)对应点为P′(x+3,y﹣4).
(1)画出平移后的图形;
(2)三角形ABC是经过怎样平移后得到三角形![]() ?
?
(3)在三角形ABC平移到![]() 的过程中,线段AB扫过的面积为 .
的过程中,线段AB扫过的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个三位数n,如果n满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为F(n).例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以F(123)=6.
(1)计算:F(243),F(617);
(2)若s,t都是“相异数”,其中s=100x+32,t=150+y(1≤x≤9,1≤y≤9,x,y都是正整数),规定:k= ![]() ,当F(s)+F(t)=18时,求k的最大值.
,当F(s)+F(t)=18时,求k的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com