
����Ŀ���̲ĵھ�����̽���˷���ʽʱ��������ͼ������IJ�ͬ��ʾ������֤�˳˷���ʽ���ҹ���������ѧ����ˬ�����ڹ�Ԫ3���ͣ��Ͱ�һ�����ηֳ��ĸ�ȫ�ȵ�ֱ�������Σ����ĸ�ȫ�ȵ�ֱ��������ƴ����һ�����������(��ͼ��)�����ͼ�γ�Ϊ��ˬ��ͼ����֤��һ���dz���Ҫ�Ľ��ۣ���ֱ������������ֱ�DZ�a��b��б��c�����ϵʽa2��b2��c2����Ϊ���ɶ�����
(1)�����Խ��С�������ĸ�ȫ�ȵ�ֱ��������ƴ������һ�����������(��ͼ��)��Ҳ����֤������ۣ��������С�������֤�Ĺ��̣�
(2)С���ְ����ĸ�ȫ�ȵ�ֱ��������ƴ����һ������(��ͼ��)����������̽�����ý��ۣ���a��3��b��4ʱ����ABCD���ܳ���
(3)��ͼ�ܣ���ÿ��С�����α߳�Ϊ1�ķ���ֽ�У���ABC�Ķ��㶼�ڷ���ֽ����ϣ�����ͼ�л�����ABC�ĸ�BD����������Ľ��ۣ����BD�ij���


���𰸡���1���������⣬���ǿ���ͼ���ҵ�����ϵ�����м��С�����ε�������ڴ������ε������ȥ�ĸ�ֱ�������ε�������г���ʽ���ɵó����ɶ����ı���ʽ����2��![]() ����3��������BD����ͼ��BD=
����3��������BD����ͼ��BD=![]()

��������
��1�������ĸ�ȫ�ȵ�ֱ�������ε����+��Ӱ����С�����ε����=�������ε������������ֵ������֤����
��2���ɣ�1���н��������c��ֵ���ٸ����ܳ���ʽ���ɵó�����ABCD���ܳ���
��3���ȸ��ݸߵĶ��廭��BD���ɣ�1���н������AC�ij����ٸ�����ABC�����������ʽ�����������BD�ij���
(1)֤������ͼ�ã�![]() ��ab��4��c2��(a��b)��(a��b)��
��ab��4��c2��(a��b)��(a��b)��
��������2ab��c2��a2��b2��2ab��
��a2��b2��c2��
(2)�⡡��a��3��b��4��
��c��![]() ��5��
��5��
����ABCD���ܳ�Ϊ��a��c��3a��c��4a��2c��4��3��2��5��22��
(3)�⡡��ͼ4��BD����ABC�ĸߣ�
��S��ABC��![]() AC��BD��
AC��BD��![]() AB��3��AC��
AB��3��AC��![]() ��5��
��5��
��BD��![]() ��
��![]() ��
��![]() .
.
�ʴ�Ϊ��(1)��������(2)22;(3)![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˳������ܵ�̼�����ij��˾�Լ��������õ��շ������¹涨��һ������һ�����õ���������aǧ��ʱ����һ���µĵ��Ϊ20Ԫ��������aǧ��ʱ������˽�20Ԫ�⣬��������ÿǧ��ʱҪ�� ![]() Ԫ��ij����3�·��õ�80ǧ��ʱ�������35Ԫ��4�·��õ�45ǧ��ʱ�������20Ԫ��
Ԫ��ij����3�·��õ�80ǧ��ʱ�������35Ԫ��4�·��õ�45ǧ��ʱ�������20Ԫ��
��1����a��ֵ��
��2����������5�·ݽ����45Ԫ����ô�����ᵱ���õ���Ϊ����ǧ��ʱ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����6��������ƴ�ɵ�һ�������Σ������С�������εı߳�Ϊ1
(��)�ܷ����ƴ�ɵij����ε������____(������������������)��
(��)���ܣ�����д��ƴ�ɵij����ε�����������ܣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��վ����A��B�������������շѷ�ʽ��
�շѷ�ʽ | ��ʹ�÷�/Ԫ | ��ʱ����ʱ��/h | ��ʱ��/��Ԫ/min�� |
A | 30 | 25 | 0.05 |
B | m | n | P |
��ÿ������ѧϰʱ��Ϊx��h��Сʱ������A��B���շѽ��ֱ�ΪyA ��Ԫ����yB��Ԫ����
��ͼ��yB��x֮�亯����ϵ��ͼ��
��������ʾ�����ۼ�����ʱ�䲻��������ʱ����ʱ�䡱����ֻ�ա���ʹ�÷ѡ������ۼ�����ʱ�䲻��������ʱ����ʱ�䡱����Գ��������ټ��ա���ʱ�ѡ���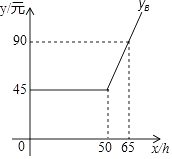
��1��m=��n=p= ��
��2��д��yA��x֮��ĺ�����ϵʽ��
��3����ÿ��������ʱ��Ϊ29Сʱ����˵��ѡȡ���ַ�ʽ�ܽ�ʡ�����ѣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬��A=30�㣮��D��AB�е㣬��EΪ��AC��һ�㣬����CD��DE����DEΪ����DE��������ȱ�������DEF������BF��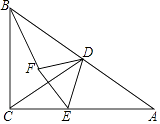
��1����BCD����״Ϊ��
��2�����ŵ�Eλ�õı仯����DBF�Ķ����Ƿ�仯�������ͼ˵��������ɣ�
��3������F���ڱ�AC��ʱ����AC=6����ֱ��д��DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�ٰ���꼶ѧ����ѧ�������������������ĸ���Ŀ�����ɰ�ƴͼ��Ȥ���ɽ⣬��ѧӦ�ã�ħ����ԭ��ÿ����Ŀ�÷ֶ���һ���ٷֱ����������ܷ֣��±�Ϊ�ף��ң�����λͬѧ�÷��������λ���֣�
���ɰ�ƴͼ | Ȥ���ɽ� | ��ѧӦ�� | ħ����ԭ | |
�� | 66 | 89 | 86 | 68 |
�� | 66 | 60 | 80 | 68 |
�� | 66 | 80 | 90 | 68 |
��1�������ײ²����ɰ�ƴͼ��Ȥ���ɽ⣬��ѧӦ�ã�ħ����ԭ���ĸ���Ŀ�÷ֱַ�10%��40%��20%��30%����������ܷ֣����ݲ²⣬������ܷ֣�
��2�����δ�����ί�����������ܷ�Ϊ80�����ϣ�����80�֣���ѧ����һ�Ƚ����ֻ�Ϥ�ң������ֱַܷ���70�֣�80�֣������ɰ�ƴͼ��ħ����ԭ����÷������ķ�������20�֣��ʼ��ܷ�����α�����һ�Ƚ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪�����������ϣ�|a|��ʾ��a��ԭ��ľ��룬���Ǿ���ֵ�ļ� �����壬��һ���أ�������������A��B���ֱ���a ��b ��ʾ����ôA��B����֮��ľ���ΪAB��|a��b|���ô˽��ۣ��ش��������⣺
(1)�����ϱ�ʾ3 ��7 ������֮��ľ����� �������ϱ�ʾ��3 �ͩ�7 ���� ��֮��ľ����� �������ϱ�ʾ2 �ͩ�3 ������֮��ľ����� ��
(2)�����ϱ�ʾx�ͩ�5 ������A��B֮��ľ����� �����|AB|��3���� ôx��ֵΪ ��
(3)������ʽ|x��1|+|x��3|ȡ��Сֵʱ����Ӧ��x��ȡֵ��Χ�Ƕ��٣���Сֵ�Ƕ��٣�
(4)��֪��A�������϶�Ӧ������a����B�������϶�Ӧ������b����|a+4|+(b��1)2��0�����P�������϶�Ӧ������x����|PA|��|PB|��2ʱ����x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�������������շѷ������û�����ѡ��һ��AΪ��ʱ��--1Ԫ![]() ʱ��BΪ������--80Ԫ
ʱ��BΪ������--80Ԫ![]() �£�����ÿ��������ʽ������ͨѶ��
�£�����ÿ��������ʽ������ͨѶ��![]() Ԫ
Ԫ![]() ʱ��
ʱ��
![]() ij�û�ÿ������40Сʱ��ѡ���ַ�ʽ�ȽϺ��ʣ�
ij�û�ÿ������40Сʱ��ѡ���ַ�ʽ�ȽϺ��ʣ�
![]() ij�û�ÿ����100ԪǮ����������ѡ���ַ�ʽ�ȽϺ��㣿
ij�û�ÿ����100ԪǮ����������ѡ���ַ�ʽ�ȽϺ��㣿
![]() �������һ��������ʹ�û��ܺ�����ѡ��������ʽ��
�������һ��������ʹ�û��ܺ�����ѡ��������ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ա�DEB����E��AB����DE��AC�ཻ�ڵ�F.
(1)��DE��8��BC��5ʱ���߶�AE�ij�Ϊ____��
(2)����D��35�㣬��C��60�㣬���DBC�Ķ�����

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com