
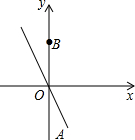
 已知正比例函数过点A(2,-4),点P在正比例函数图象上,B(0,4)且S△ABP=8.
已知正比例函数过点A(2,-4),点P在正比例函数图象上,B(0,4)且S△ABP=8.分析 (1)设正比例函数的解析式为y=kx(k≠0),再把A(2,-4)代入即可求出k的值;
(2)设出P点坐标,再分x<0与x>0两种情况进行讨论.
解答 解:(1)设正比例函数为y=kx(k≠0),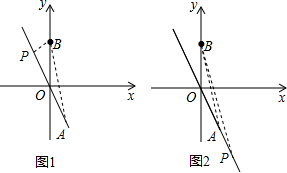
∵A(2,-4),
∴-4=2k,解得k=-2,
∴正比例函数的解析式为:y=-2x.
(2)设P(x,-2x)
如图1所示,当x<0时,S△ABP=S△PBO+S△ABO=-4x÷2+4×2÷2=8,
解得x=-2,
∴P(-2,4);
②如图2所示,
当x>0时 S△ABP=S△PBO-S△ABO=4x÷2-4×2÷2=8,
解得x=6.
∴P(6,-12).
综上所述,P点坐标为(-2,4),(6,-12).
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
 已知:如图.
已知:如图.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
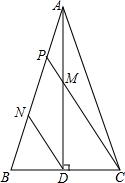 如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,点M是线段AD的中点,CM交AB于点P,DN∥CM交AB于点N,若AB=6,求PN的长.
如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,点M是线段AD的中点,CM交AB于点P,DN∥CM交AB于点N,若AB=6,求PN的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
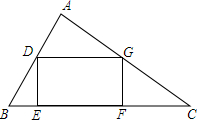 如图,已知△ABC中,BC=24,在△ABC中截出一个矩形DEFG,已知矩形的面积S与EF的长x满足关系式:S=-$\frac{2}{3}$x2+16x,问:EF的长为多少时,矩形的面积等于72?
如图,已知△ABC中,BC=24,在△ABC中截出一个矩形DEFG,已知矩形的面积S与EF的长x满足关系式:S=-$\frac{2}{3}$x2+16x,问:EF的长为多少时,矩形的面积等于72?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com