
分析 (1)原来一天可获利润=(原售价-原进价)×一天的销售量;
(2)①根据等量关系:降价后的单件利润×销售量=总利润,列方程解答;
②根据“总利润=降价后的单件利润×销售量”列出函数表达式,并运用二次函数性质解答.
解答 解:(1)(100-80)×100=2000(元);
故答案为:2000.
(2)①依题意得:
(100-80-x)(100+10x)=2160
即x2-10x+16=0
解得:x1=2,x2=8
经检验:x1=2,x2=8都是方程的解,且符合题意.
答:商店经营该商品一天要获利润2160元,则每件商品应降价2元或8元.
②依题意得:y=(100-80-x)(100+10x),
∴y=-10x2+100x+2000=-10(x-5)2+2250,
∵-10≤0,
∴当x=5时,商店所获利润最大.
点评 本题考查了一元二次方程和二次函数的应用,解答第②小题的关键是将实际问题转化为二次函数求解,注意配方法求二次函数最值的应用.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源:2016-2017学年福建省泉州市泉港区2016-2017学年八年级3月教学质量检测数学试卷(解析版) 题型:单选题
若点P(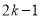 ,
,  )在第二象限,则k的取值范围是( )
)在第二象限,则k的取值范围是( )
A. 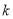 <
<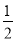 B.
B.  <2 C.
<2 C.  <
<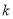 <2 D.
<2 D. 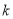 >2
>2
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
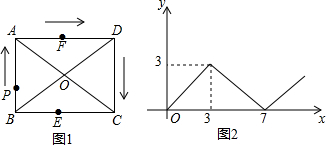 如图,矩形ABCD中,对角线AC,BD交于点O,E,F分别是边BC,AD的中点,AB=3,BC=4,一动点P从点B出发,沿着B-A-D-C在矩形的边上运动,运动到点C停止,点M为图1中某一定点,设点P运动的路程为x,△BPM的面积为y,表示y与x的函数关系的图象大致如图2所示.则点M的位置可能是图1中的( )
如图,矩形ABCD中,对角线AC,BD交于点O,E,F分别是边BC,AD的中点,AB=3,BC=4,一动点P从点B出发,沿着B-A-D-C在矩形的边上运动,运动到点C停止,点M为图1中某一定点,设点P运动的路程为x,△BPM的面积为y,表示y与x的函数关系的图象大致如图2所示.则点M的位置可能是图1中的( )| A. | 点C | B. | 点F | C. | 点D | D. | 点O |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
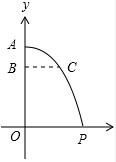 2008年7月某地区遭受严重的自然灾害,空军某部队奉命赶灾区空投物资,已知空投物资离开飞机后在空中沿抛物线降落,抛物线顶点为机舱航口A,如图所示,如果空投物资离开A处后下落的垂直高度AB=160米时,它测A处的水平距离BC=200米,那么要使飞机在垂直高度AO=1000米的高空进行空投,物资恰好准确地落在居民点P处,飞机到P处的水平距离OP应为500米.
2008年7月某地区遭受严重的自然灾害,空军某部队奉命赶灾区空投物资,已知空投物资离开飞机后在空中沿抛物线降落,抛物线顶点为机舱航口A,如图所示,如果空投物资离开A处后下落的垂直高度AB=160米时,它测A处的水平距离BC=200米,那么要使飞机在垂直高度AO=1000米的高空进行空投,物资恰好准确地落在居民点P处,飞机到P处的水平距离OP应为500米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
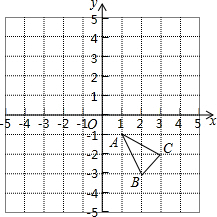 在如图所示的平面直角坐标系中,△ABC的三个顶点分别为A(1,-1),B(2,-3),C(3,-2).
在如图所示的平面直角坐标系中,△ABC的三个顶点分别为A(1,-1),B(2,-3),C(3,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ABC=90°,点D在BC的延长线上,且BD=AB,过点B作BE⊥AC,与BD的垂线DE交于点E
如图,在Rt△ABC中,∠ABC=90°,点D在BC的延长线上,且BD=AB,过点B作BE⊥AC,与BD的垂线DE交于点E查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
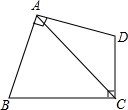 如图,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,若四边形ABCD的面积是20cm2,则AC的长是2$\sqrt{10}$cm.
如图,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,若四边形ABCD的面积是20cm2,则AC的长是2$\sqrt{10}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com