
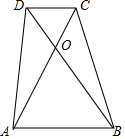
 如图,在梯形ABCD中.DC∥AB.对角线AC,BD交于O点,设S△ODC=S1,S△AOB=S2,求证:S梯形ABCD=($\sqrt{{S}_{1}}$+$\sqrt{{S}_{2}}$)2.
如图,在梯形ABCD中.DC∥AB.对角线AC,BD交于O点,设S△ODC=S1,S△AOB=S2,求证:S梯形ABCD=($\sqrt{{S}_{1}}$+$\sqrt{{S}_{2}}$)2. 分析 如图,作CM∥DB交AB的延长线于M,首先证明S△ACM=S梯形ABCD,设△ACM的面积为S,由△DOC∽△BOA∽△MCA,推出$\sqrt{{S}_{2}}$:$\sqrt{S}$=OA:AC,$\sqrt{{S}_{1}}$:$\sqrt{S}$=OC:AC,推出$\frac{\sqrt{{S}_{2}}}{\sqrt{S}}$+$\frac{\sqrt{{S}_{1}}}{\sqrt{S}}$=$\frac{OA}{AC}$+$\frac{OC}{AC}$=1,即可解决问题.
解答 证明:如图,作CM∥DB交AB的延长线于M.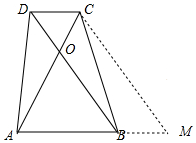
∵CD∥AM,DB∥CM,
∴四边形DBMC是平行四边形,
∴S△DCA=S△DCB=S△BCM,
∴S△ACM=S梯形ABCD,设△ACM的面积为S,
∵△DOC∽△BOA∽△MCA,
∴$\sqrt{{S}_{2}}$:$\sqrt{S}$=OA:AC,$\sqrt{{S}_{1}}$:$\sqrt{S}$=OC:AC,
∴$\frac{\sqrt{{S}_{2}}}{\sqrt{S}}$+$\frac{\sqrt{{S}_{1}}}{\sqrt{S}}$=$\frac{OA}{AC}$+$\frac{OC}{AC}$=1,
∴$\sqrt{S}$=$\sqrt{{S}_{1}}$+$\sqrt{{S}_{2}}$,
∴S梯形ABCD=S=($\sqrt{{S}_{1}}$+$\sqrt{{S}_{2}}$)2.
点评 本题考查梯形的面积、三角形的面积、平行四边形的性质等知识,解题的关键是学会添加常用辅助线,构造特殊四边形,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
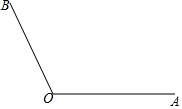 如图,已知∠AOB=120°.点C在∠AOB的内部,且∠BOC=30°;OP是∠AOB的角平分线.
如图,已知∠AOB=120°.点C在∠AOB的内部,且∠BOC=30°;OP是∠AOB的角平分线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
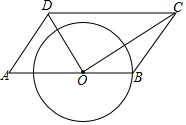 如图,平行四边形ABCD中,O为AB上的一点,连接OD、OC,以O为圆心,OB为半径画圆,分别交OD,OC于点P,Q,若OB=2,OD=3,∠ADO=∠A,$\widehat{PQ}$=π,判断直线DC与⊙O的位置关系,并说明理由.
如图,平行四边形ABCD中,O为AB上的一点,连接OD、OC,以O为圆心,OB为半径画圆,分别交OD,OC于点P,Q,若OB=2,OD=3,∠ADO=∠A,$\widehat{PQ}$=π,判断直线DC与⊙O的位置关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,如图,CD是△ABC的高,∠A=22.5°,边AC的垂直平分线交AB于点E,EF⊥BC,交CD于点G,垂足为F.
已知,如图,CD是△ABC的高,∠A=22.5°,边AC的垂直平分线交AB于点E,EF⊥BC,交CD于点G,垂足为F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
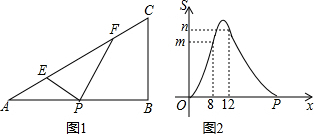
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
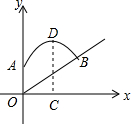 一个运动员推铅球,铅球在点A处出手,出手时铅球离地面$\frac{7}{6}$m,铅球运行时距离地面的最大高度CD是2.5m,此时铅球验水平方向行进了4m,铅球落地点在斜坡上的点B处,已知铅球经过的路线是抛物线,现以铅球出手点A所在的铅垂线OA的方向为y轴正方向,以铅垂线与地面的交点为点O建立直角坐标系,斜坡可以用一次函数y=$\frac{1}{4}$x刻画.
一个运动员推铅球,铅球在点A处出手,出手时铅球离地面$\frac{7}{6}$m,铅球运行时距离地面的最大高度CD是2.5m,此时铅球验水平方向行进了4m,铅球落地点在斜坡上的点B处,已知铅球经过的路线是抛物线,现以铅球出手点A所在的铅垂线OA的方向为y轴正方向,以铅垂线与地面的交点为点O建立直角坐标系,斜坡可以用一次函数y=$\frac{1}{4}$x刻画.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com