
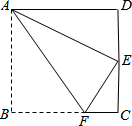
 如图所示,四边形ABCD为长方形纸片,把纸片ABCD折叠,使点B恰好落在CD边的中点E处,折痕为AF,CD=6,求AF的长.
如图所示,四边形ABCD为长方形纸片,把纸片ABCD折叠,使点B恰好落在CD边的中点E处,折痕为AF,CD=6,求AF的长. 分析 由翻折的性质可知:AB=AE=6,△ADE中由勾股定理可求得AD的长,然后在△EFC中由勾股定理可求得FC的长,最后再△ABF中利用勾股定理可求得AF的长.
解答 解:由翻折的性质可知:AB=AE=6,BF=EF.
∵E是CD的中点,
∴DE=3.
在Rt△ADE中,由勾股定理得:AD=$\sqrt{A{E}^{2}-D{E}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$.
设FC=x,则EF=3$\sqrt{3}$-x.
在Rt△EFC中,由勾股定理得;FC2+EC2=EF2,即:${x}^{2}+{3}^{3}=(3\sqrt{3}-x)^{2}$.
解得;x=$\sqrt{3}$.
∴BF=2$\sqrt{3}$.
在Rt△ABF中,由勾股定理得:AF=$\sqrt{A{B}^{2}+B{F}^{2}}$=$\sqrt{{6}^{2}+(2\sqrt{3})^{2}}$=4$\sqrt{3}$.
点评 本题主要考查的是翻折的性质、勾股定理的应用,利用勾股定理分别求得AD、FC的长是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
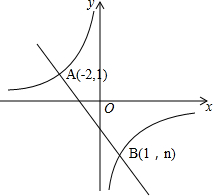 如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象相交于A、B两点,
如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象相交于A、B两点,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
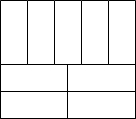 某居民小区为了绿化小区环境,建设和谐家园.准备将一块周长为76米的长方形空地,设计成长和宽分别相等的9块小长方形,如图所示.计划在空地上种上各种花卉,经市场预测,绿化每平方米空地造价110元,请计算,要完成这块绿化工程,预计花费多少元?
某居民小区为了绿化小区环境,建设和谐家园.准备将一块周长为76米的长方形空地,设计成长和宽分别相等的9块小长方形,如图所示.计划在空地上种上各种花卉,经市场预测,绿化每平方米空地造价110元,请计算,要完成这块绿化工程,预计花费多少元?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com