
 某校数学兴趣小组用高为1.5米的仪器测量建筑物CD的高度,如图,由距CD一定距离的A处用仪器观察建筑物顶部D的仰角为β,在A和C之间选一点B,由B处用仪器观察建筑物顶部D的仰角为α,测得A、B之间的距离为2米,tanα=$\frac{6}{5}$,tanβ=$\frac{10}{9}$,试求建筑物CD的高度.
某校数学兴趣小组用高为1.5米的仪器测量建筑物CD的高度,如图,由距CD一定距离的A处用仪器观察建筑物顶部D的仰角为β,在A和C之间选一点B,由B处用仪器观察建筑物顶部D的仰角为α,测得A、B之间的距离为2米,tanα=$\frac{6}{5}$,tanβ=$\frac{10}{9}$,试求建筑物CD的高度. 分析 CD与EF的延长线交于点G,设DG=x米.由三角函数的定义得到,在Rt△DGF中,tanα=$\frac{DG}{GF}$,在Rt△DGE中,tanβ=$\frac{DG}{GE}$,根据EF=EG-FG,得到关于x的方程,解出x,再加上1.5即为建筑物CD的高度.
解答  解:CD与EF的延长线交于点G,如图,设DG=x米.
解:CD与EF的延长线交于点G,如图,设DG=x米.
在Rt△DGF中,tanα=$\frac{DG}{GF}$,即tanα=$\frac{x}{GF}$.
在Rt△DGE中,tanβ=$\frac{DG}{GE}$,即tanβ=$\frac{x}{GE}$.
∴GF=$\frac{x}{tanα}$,GE=$\frac{x}{tanβ}$,
∴EF=$\frac{x}{tanβ}$-$\frac{x}{tanα}$.
∴2=$\frac{9x}{10}$-$\frac{5x}{6}$,
解方程得:x=30.
∴CD=DG+GC=30+1.5=31.5.
答:建筑物高为31.5米.
点评 本题考查了解直角三角形-仰角的概念:向上看,视线与水平线的夹角叫仰角.也考查了测量建筑物高度的方法以及三角函数的定义.


科目:初中数学 来源: 题型:解答题
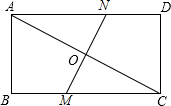 如图,在矩形ABCD中,AB=6,BC=8,将矩形ABCD折叠,使点C与点A重合,折痕交BC于M,交AC于O,交AD于N,求:
如图,在矩形ABCD中,AB=6,BC=8,将矩形ABCD折叠,使点C与点A重合,折痕交BC于M,交AC于O,交AD于N,求:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB于E,若AC=10cm,则BD+DE=( )
如图,△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB于E,若AC=10cm,则BD+DE=( )| A. | 10cm | B. | 8cm | C. | 6cm | D. | 9cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
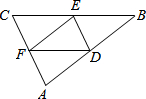 如图,在△ABC中,点D、E、F分别是AB、BC、CA的中点,若△ABC的周长为10cm,则△DEF的周长是( )
如图,在△ABC中,点D、E、F分别是AB、BC、CA的中点,若△ABC的周长为10cm,则△DEF的周长是( )| A. | 8cm | B. | 6cm | C. | 5cm | D. | 4cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
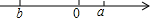 已知实数,在数轴上的位置如图所示,则以下三个命题:①a3-ab2<0,②$\sqrt{{{(a+b)}^2}}=a+b$,③$\frac{1}{a+b}<\frac{1}{a}$,其中真命题的序号为①.
已知实数,在数轴上的位置如图所示,则以下三个命题:①a3-ab2<0,②$\sqrt{{{(a+b)}^2}}=a+b$,③$\frac{1}{a+b}<\frac{1}{a}$,其中真命题的序号为①.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
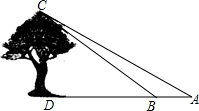 大庄中学9年级学生在学习“解直角三角形”一章时,开展测量物体高度的实践活动,他们要测量校园内一棵大树的高度.如图,在大树前的平地上选一点A,测得由点A看大树顶端C的仰角为35°,在点A和大树之间选择一点B(A,B,D在同一直线上),测得由点B看大树顶端C的仰角为45°,再量得A,B两点间的距离为5.43米,求大树CD的高度(结果精确到0.1米).(测角器的高度忽略不计.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin45°≈0.71,cos45°≈0.71)
大庄中学9年级学生在学习“解直角三角形”一章时,开展测量物体高度的实践活动,他们要测量校园内一棵大树的高度.如图,在大树前的平地上选一点A,测得由点A看大树顶端C的仰角为35°,在点A和大树之间选择一点B(A,B,D在同一直线上),测得由点B看大树顶端C的仰角为45°,再量得A,B两点间的距离为5.43米,求大树CD的高度(结果精确到0.1米).(测角器的高度忽略不计.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin45°≈0.71,cos45°≈0.71)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com