
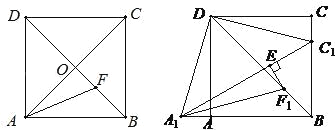
����Ŀ����ͼ����������ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AFƽ�֡�BAC����BD�ڵ�F��
��1����֤��![]() ��
��
��2����A1����C1�ֱ�ͬʱ��A��C�������������ͬ���ٶ��˶���ͬ��ʱ���ͬʱֹͣ����ͼ��A1F1ƽ�֡�BA1C1����BD�ڵ�F1������F1��F1E��A1C1������ΪE�������EF1��AB��![]() ����֮���������ϵ����֤����IJ��룻
����֮���������ϵ����֤����IJ��룻
��3���ڣ�2���������£���A1E��6��C1E��4ʱ����BD�ij�Ϊ������
���𰸡���1���������� ��2��AB��EF1��![]() A1C1 �����ɼ���������3��
A1C1 �����ɼ���������3��![]()
�����������������
��1������ͼ������F��FG��AB�ڵ�G������AFƽ�֡�CAB���ı���ABCD����������֤��AOF�ա�AGF����BGF�ǵ���ֱ�������Σ��ɴ˿ɵ�AO=AG��FG=BG=OF���Ӷ��ɵ�AB=AG+BG=AO+OF=![]() AC+OF�����μ��ɵõ�������
AC+OF�����μ��ɵõ�������
��2������ͼ����F1��F1G1��A1B����F1��F1H1��BC1�ɴ˿ɵ��ı���F1G1BH1�Ǿ��Σ�
����֪������EF1��G1F1��F1H1���Ӷ��ɵ�F1��������A1BC1�����ģ��ɡ�ֱ������������Բ�İ뾶�������߳���Ĺ�ϵ�����CC1=AA1���������EF1��AB��![]() ����֮���������ϵ��
����֮���������ϵ��
��3����ͼ����CC1=AA1=x���ɵ�F1�ǡ�A1BC1�����ģ���E1��G1��H1�����е�ɵ�A1E����A1C1��A1B��BC1����2����A1E��[A1C1����AB��x������AB��x��]��2����10��2x����2��6��
�ɴ˽��x��1��Ȼ����Rt��A1BC1�У���A1B2��BC12��AC12���ɵ�����AB��1��2����AB��1��2��100�����AB�ij�������BD=![]() AB���BD�ij�.
AB���BD�ij�.
���������
��1����F��FG��AB��G��
��AFƽ�֡�CAB��FO��AC��FG��AB��
��OF��FG��
�ߡ�AOF����AGF��90�㣬AF��AF��OF��FG��
���AOF�ա�AGF��
��AO��AG��
ֱ��������BGF�У���DGA��45�㣬
��FG��BG��OF��
��AB��AG��BG��AO��OF��![]() AC��OF��
AC��OF��
��AB��OF��![]() AC��
AC��
��2����F1��F1G1��A1B����F1��F1H1��BC1�����ı���F1G1BH1�Ǿ��Σ�
��BDƽ����ABC��A1F1ƽ�֡�BA1C1��
��F1H1��F1G1=EF1��
����F1��������A1BC1�����ģ�
��EF1����A1B��BC1��A1C1����2����
��A1B��BC1��AB��A1A��BC��CC1����CC1��A1A��
��A1B��BC1��2AB��
��ˢ�ʽ��д�ɣ�EF1����2AB��A1C1����2��
��AB��EF1��![]() A1C1��
A1C1��

��3���ɣ�2���ã�F1��������A1BC1�����ģ���E1��G1��H1�����е㣮
��A1E����A1C1��A1B��BC1����2��
�����CC1��A1A��x��
A1E��[A1C1����AB��x������AB��x��]��2����10��2x����2��6��
��x��1��
��ֱ��������A1BC1�У����ݹ��ɶ�����A1B2��BC12��AC12��
������AB��1��2����AB��1��2��100��
���AB��7��
��BD��7![]() ��
��




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ų�¼Ƭ��֮�¡��IJ�����ȫ���Կ�����Ⱦ����Խ��Խ���ӣ�����������������Ҳ��������������ӳ��ҹ�����A��B�����ͺŵĿ�������������֪һ̨A�Ϳ����������Ľ��۱�һ̨B�Ϳ����������Ľ��۶�300Ԫ����7500Ԫ����A�Ϳ�������������6000Ԫ����B�Ϳ�����������̨����ͬ��
��1����һ̨A�Ϳ�����������һ̨B�Ϳ����������Ľ��۸�Ϊ����Ԫ��
��2�������۹����У�A�Ϳ�����������Ϊ��������ǿ������С�����������ߵĻ�ӭ��Ϊ������B�Ϳ������������������������������B�Ϳ������������н������ۣ����г����飬��B�Ϳ������������ۼ�Ϊ1800Ԫʱ��ÿ�������4̨���ڴ˻����ϣ��ۼ�ÿ����50Ԫ��ÿ�콫���۳�1̨�����ÿ�������������B�Ϳ���������������Ϊ3200Ԫ�������������Ӧ��B�Ϳ������������ۼ۶�Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������a��b��2��2+|a+b+3|=0����a2��b2��ֵ�ǣ�������
A. ��1 B. 1 C. 6 D. ��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=ax2+bx+c�Ķ���A��x���ϣ���y��Ľ���B��0��-1������b=-4ac��
��1�����A�����ꣻ
��2���������ߵĽ���ʽ
��3�������������Ƿ����һ��C��ʹ��BCΪֱ����Բ���������ߵĶ���A������������˵�����ɣ������ڣ������C�����꣬�������ʱԲ��Բ�ĵ�е����ꡣ

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��һ�κ���y=kx+b��ͼ���뷴��������y=![]() ��ͼ������A��3��-2���͵�B��n��6����
��ͼ������A��3��-2���͵�B��n��6����
��1��n= ��
��2������������������ʽ
��3��ֱ��д��һ�κ���ֵ���ڷ���������ֵ���Ա���x��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ����Ӱչ�������䶫���������һ�����A��B������Ϊ����C������ֱ�����������D��E����Ӱ������֣����ѡһ����ڽ���չ�������ι۽�������ѡһ�������뿪��
��1��֣�ƴӽ��뵽�뿪���ж����ֿ��ܵĽ�����뻭������ͼ��
��2�����֣�ƴ����A����չ�������ӱ�������뿪�ĸ��ʡ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ABCD�У�E��CD����һ�㣬
��1������ADE�Ƶ�A��˳ʱ�뷽����ת��ʹAD��AB�غϣ��õ���ABF����ͼ1��ʾ���۲��֪����DE��ȵ��߶����� ������AFB=���� ��
��2����ͼ2��������ABCD�У�P��Q�ֱ���BC��CD���ϵĵ㣬�ҡ�PAQ=45������ͨ����ת�ķ�ʽ˵����DQ+BP=PQ��
��3���ڣ�2�����У�����BD�ֱ�AP��AQ��M��N���㻹������ת��˼��˵��BM2+DN2=MN2��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com