
 附加题:如图△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD于E,连接AE.
附加题:如图△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD于E,连接AE.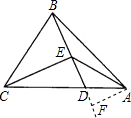 解:(1)在Rt△CED中,∠BDC=60°,
解:(1)在Rt△CED中,∠BDC=60°,| CD |
| 2 |
| 3 |
| 3 |
| 3 |
| AF |
| AE |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| S△BEC |
| S△BEA |
| ||
|
| CE |
| AF |
| ||||
|


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源:2010-2011学年四川省眉山市丹棱县张场中学九年级(上)期中数学试卷(解析版) 题型:解答题
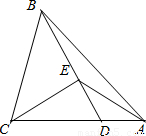
查看答案和解析>>
科目:初中数学 来源:第19章《相似形》常考题集(08):19.5 相似三角形的判定(解析版) 题型:解答题
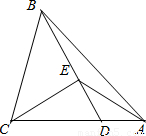
查看答案和解析>>
科目:初中数学 来源:2004年全国中考数学试题汇编《三角形》(12)(解析版) 题型:解答题
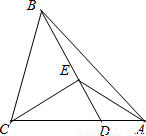
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com