
如图,AB是⊙O的直径,点C,D是半圆O的三等分点,过点C作⊙O的切线交AD的延长线于点E,过点D作DF⊥AB于点F,交⊙O于点H,连接DC,AC.
(1)求证:∠AEC=90°;
(2)试判断以点A,O,C,D为顶点的四边形的形状,并说明理由;
(3)若DC=2,求DH的长.
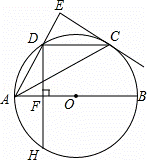
解:(1)连接OC,
∵EC与⊙O切点C,
∴OC⊥EC,
∴∠OCE=90°,
∵点CD是半圆O的三等分点,
∴ =
= =
= ,
,
∴∠DAC=∠CAB,
∵OA=OC,
∴∠CAB=∠OCA,
∴∠DAC=∠OCA,
∴AE∥OC(内错角相等,两直线平行)
∴∠AEC+∠OCE=180°,
∴∠AEC=90°;
(2)四边形AOCD为菱形.
理由是:
∵ =
= ,
,
∴∠DCA=∠CAB,
∴CD∥OA,
又∵AE∥OC,
∴四边形AOCD是平行四边形,
∵OA=OC,
∴平行四边形AOCD是菱形(一组邻边相等的平行四边形是菱形);
(3)连接OD.
∵四边形AOCD为菱形,
∴OA=AD=DC=2,
∵OA=OD,
∴OA=OD=AD=2,
∴△OAD是等边三角形,
∴∠AOD=60°,
∵DH⊥AB于点F,AB为直径,
∴DH=2DF,
在Rt△OFD中,sin∠AOD= ,
,
∴DF=ODsin∠AOD=2sin60°=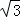 ,
,
∴DH=2DF=2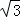 .
.



 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
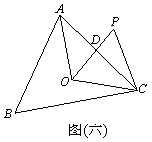
如图(六),O为△ABC的外心,△OCP为正三角形, 与
与 相交于D点,连接
相交于D点,连接 。若ÐBAC=70°,
。若ÐBAC=70°, =
= ,则ÐADP的度数为何?
,则ÐADP的度数为何?
(A) 85 (B) 90 (C) 95 (D) 110
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
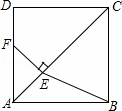
如图,在正方形ABCD中,点E是对角线AC上一点,且CE=CD,过点E作EF⊥AC交AD于点F,连接BE.
(1)求证:DF=AE;
(2)当AB=2时,求BE2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
地球与月球的平均距离大约为384000km,将384000用科学记数法表示应为( )
|
| A. | 0.384×106 | B. | 3.84×106 | C. | 3.84×105 | D. | 384×103 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com