
【题目】如图,在锐角![]() 中,以
中,以![]() 为直径的
为直径的![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的切线
的切线![]() 交边
交边![]() 于点
于点![]() ,连结
,连结![]() .
.
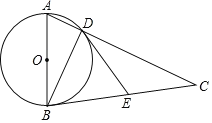
(1)求证:![]() .
.
(2)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接OD,如图,首先利用切线的性质,得![]() ;然后利用圆周角定理的推论,得
;然后利用圆周角定理的推论,得![]() ,则
,则![]() ;再根据等腰三角形的性质,得
;再根据等腰三角形的性质,得![]() ,从而得
,从而得![]() .
.
(2)过E作![]() 于H,如图,首先由已知
于H,如图,首先由已知![]() ,
,![]() ,得
,得![]() 和
和![]() 的长度;然后在Rt△ABD中,利用
的长度;然后在Rt△ABD中,利用![]() 和正切的定义,得
和正切的定义,得![]() 的长,在Rt△CDB和Rt△ABD中,根据正切的定义得到
的长,在Rt△CDB和Rt△ABD中,根据正切的定义得到![]() 和
和![]() 的值,由
的值,由![]() ,即可得
,即可得![]() 的值;设
的值;设![]() ,在Rt△CHE和Rt△DHE中,分别根据
,在Rt△CHE和Rt△DHE中,分别根据![]() 、
、![]() 的值和正切的定义,用含x的式子表示出
的值和正切的定义,用含x的式子表示出![]() 和
和![]() ,再根据
,再根据![]() 的长度关系,列出方程求得x的值,然后在在Rt△DHE中,利用勾股定理即可计算出DE的长.
的长度关系,列出方程求得x的值,然后在在Rt△DHE中,利用勾股定理即可计算出DE的长.
(1)如图,连结![]() ,
,
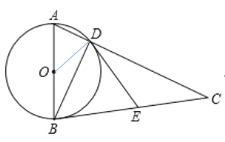
∵![]() 是切线,∴OD⊥DE,
是切线,∴OD⊥DE,
∴![]() ,
,
∵![]() 是直径,∴
是直径,∴![]()
∴![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() .
.
(2)如图,过E作![]() 于H,
于H,
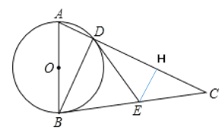
∵![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
又∵![]() ,
,
∴在Rt△ABD中,![]() ,
,
∴在Rt△CDB中,![]() ;在Rt△ABD中,
;在Rt△ABD中,![]() ,
,
∵![]() ,
,
∴![]() ,
,
设![]() ,则在Rt△CHE中,
,则在Rt△CHE中,![]() ;在Rt△DHE中,
;在Rt△DHE中,![]() ,
,
∵![]() ,∴
,∴![]() ,解得
,解得![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 中,对角线
中,对角线![]() 交于点
交于点![]() ,折叠正方形纸片,使
,折叠正方形纸片,使![]() 落在
落在![]() 上,点
上,点![]() 恰好与
恰好与![]() 上的点
上的点![]() 重合,展开后折痕
重合,展开后折痕![]() 分别交
分别交![]() 于点
于点![]() ,连
,连![]() 给出下列结论,其中正确的个数有( )
给出下列结论,其中正确的个数有( )
①![]() ;②
;②![]() ;③四边形
;③四边形![]() 是菱形;④
是菱形;④![]() .
.
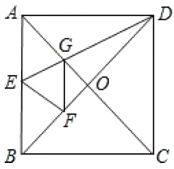
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在![]() 地时距地面的高度
地时距地面的高度![]() 为 米;
为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数关系式.
(分)之间的函数关系式.
(3)登山多长时间时,甲、乙两人距地面的高度差为50米?

查看答案和解析>>
科目:初中数学 来源: 题型:
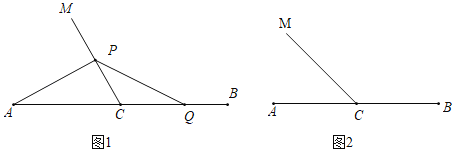
【题目】已知C为线段AB中点,∠ACM=α.Q为线段BC上一动点(不与点B重合),点P在射线CM上,连接PA,PQ,记BQ=kCP.
(1)若α=60°,k=1,
①如图1,当Q为BC中点时,求∠PAC的度数;
②直接写出PA、PQ的数量关系;
(2)如图2,当α=45°时.探究是否存在常数k,使得②中的结论仍成立?若存在,写出k的值并证明;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,点F为BE的中点,连接CF,DF.

(1)如图1,当点D在AB上,点E在AC上时
①证明:△BFC是等腰三角形;
②请判断线段CF,DF的关系?并说明理由;
(2)如图2,将图1中的△ADE绕点A旋转到图2位置时,请判断(1)中②的结论是否仍然成立?并证明你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象过点A(3,0),对称轴为直线x=1,给出以下结论:①abc<0;②3a+c=0;③ax2+bx≤a+b;④若M(﹣0.5,y1)、N(2.5,y2)为函数图象上的两点,则y1<y2.其中正确的是( )
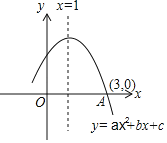
A.①③④B.①②3④C.①②③D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某新建火车站站前广场需要绿化的面积为46000米2,施工队在绿化了22000米2后,将每天的工作量增加为原来的1.5倍,结果提前4天完成了该项绿化工程.
(1)该项绿化工程原计划每天完成多少米2?
(2)该项绿化工程中有一块长为20米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56米2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),问人行通道的宽度是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
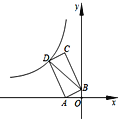
【题目】如图,点A(-2,0),B(0,1),以线段AB为边在第二象限作矩形ABCD,双曲线![]() (k<0)经过点D,连接BD,若四边形OADB的面积为6,则k的值是_____.
(k<0)经过点D,连接BD,若四边形OADB的面积为6,则k的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
①![]() 的值为 ;
的值为 ;
②∠AMB的度数为 .
(2)类比探究
如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断![]() 的值及∠AMB的度数,并说明理由;
的值及∠AMB的度数,并说明理由;
(3)拓展延伸
在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=![]() ,请直接写出当点C与点M重合时AC的长.
,请直接写出当点C与点M重合时AC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com