
【题目】如图,O在等边△ABC内,∠AOB=100°,∠BOC=x,将△BOC绕点C顺时针旋转60°,得△ADC,连接OD.
(1)△COD的形状是 ;
(2)当x=150°时,△AOD的形状是 ;此时若OB=3,OC=5,求OA的长;
(3)当x为多少度时,△AOD为等腰三角形.
【答案】(1)等边三角形;(2)直角三角形,OA=![]() ;(3)x=100°,x=130°,x=160°时,△AOD为等腰三角形.
;(3)x=100°,x=130°,x=160°时,△AOD为等腰三角形.
【解析】
(1)由旋转的性质得出CO=CD、∠OCD=60°即可知△COD是等边三角形;
(2)由旋转可以得出OC=DC,∠DCO=60°,就可以得出△ODC是等边三角形,就可以得出∠ODC=60°,从而得出∠ADO=90°,而得出△AOD的形状;最后用勾股定理即可求出OA;
(3)由条件可以表示出∠AOC=250°-a,就有∠AOD=190°-a,∠ADO=a-60°,当∠DAO=∠DOA,∠AOD=ADO或∠OAD=∠ODA时分别求出a的值即可.
解:(1)△COD是等边三角形,
∵△BOC绕点C按顺时针方向旋转60°得△ADC,
∴△BOC≌△ADC,∠OCD=60°
∴CO=CD
∴△COD是等边三角形.
故答案为:等边三角形;
(2)当α=150°时,△AOD是直角三角形.
∵△BOC绕点C按顺时针方向旋转60°得△ADC
∴△BOC≌△ADC,
∴∠BOC=∠ADC=150°
由(1)△COD是等边三角形
∴∠ODC=60°
∴∠ADO=150°﹣60°=90°
当α=150°时,△AOD是直角三角形.
由旋转知,AD=OB=3,
∵△COD是等边三角形,
∴OD=OC=3,
在Rt△AOD中,根据勾股定理得,OA=![]() =
=![]() ;
;
故答案为:直角三角形;
(3)∵∠AOB=100°,∠BOC=x,
∴∠AOC=260°﹣x.
∵△OCD是等边三角形,
∴∠DOC=∠ODC=60°,
∴∠ADO=x﹣60°,∠AOD=200°﹣x,
①当∠DAO=∠DOA时,
2(200°﹣x)+x﹣60°=180°,
解得:x=160°
②当∠AOD=ADO时,
200°﹣x=x﹣60°,
解得:x=130°,
③当∠OAD=∠ODA时,
200°﹣x+2(x﹣60°)=180°,
解得:x=100°
∴x=100°,x=130°,x=160°△AOD为等腰三角形.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】已知A(2,1)、B(3,5)、C(5,-2)、D(0,1)、E(-1,5)、F(-3,-2),则△ABC与△DEF( )
A. 关于x轴对称 B. 关于直线x=1对称
C. 关于点(1,0)对称 D. 以上答案都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
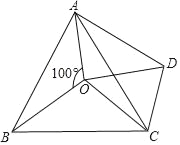
【题目】△ABC是一张等腰直角三角形纸板,∠C=90°,AC=BC=2, 
(1)要在这张纸板中剪出一个尽可能大的正方形,有甲、乙两种剪法(如图1),比较甲、乙两种剪法,哪种剪法所得的正方形面积大?请说明理由.
(2)图1中甲种剪法称为第1次剪取,记所得正方形面积为s1;按照甲种剪法,在余下的△ADE和△BDF中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为s2(如图2),则s2=;再在余下的四个三角形中,用同样方法分别剪取正方形,得到四个相同的正方形,称为第3次剪取,并记这四个正方形面积和为s3 , 继续操作下去…,则第10次剪取时,s10=;
(3)求第10次剪取后,余下的所有小三角形的面积之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=7cm,BC=3cm,CD为AB边上的高.点E从点B出发在直线BC上以2cm/s的速度移动,过点E作BC的垂线交直线CD于点F.当点E运动________s时,CF=AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=6cm,DE=2cm,则BC= . 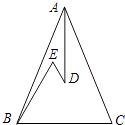
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①(﹣2)101+(﹣2)100=﹣2100;②20172+2017一定可以被2018整除;③16.9×![]() +15.1×
+15.1×![]() 能被4整除;④两个连续奇数的平方差是8的倍数.其中说法正确的个数是( )
能被4整除;④两个连续奇数的平方差是8的倍数.其中说法正确的个数是( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为 ![]() .在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O′B′.
.在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O′B′. 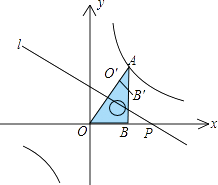
(1)当点O′与点A重合时,点P的坐标是;
(2)设P(t,0),当O′B′与双曲线有交点时,t的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】回答下列问题:
(1)如图所示的甲、乙两个平面图形能折什么几何体?
(2)由多个平面围成的几何体叫做多面体.若一个多面体的面数为f,顶点个数为v,棱数为e,分别计算第(1)题中两个多面体的f+v﹣e的值?你发现什么规律?
(3)应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com