
 =
= =
=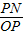 ,cos∠AOC=
,cos∠AOC= =
= =
= ,求出PN=
,求出PN= t,ON=
t,ON= t,即可得出答案;②当P在AB上时,即可得出P的纵坐标是4,横坐标是2t-5.
t,即可得出答案;②当P在AB上时,即可得出P的纵坐标是4,横坐标是2t-5. ,
, x.
x. ,
, (x-0)(x-12)=-
(x-0)(x-12)=-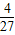 x2+
x2+ x,
x, x2+
x2+ x.
x. x2+
x2+ x=-
x=- (x-6)2+
(x-6)2+ ,
, 过A作AH⊥OC于H,PN⊥OC于N,
过A作AH⊥OC于H,PN⊥OC于N, =
= =
= ,cos∠AOC=
,cos∠AOC= =
= =
=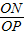 ,
, t,ON=
t,ON= t,
t, t,
t, t);
t); =6.5
=6.5

科目:初中数学 来源: 题型:
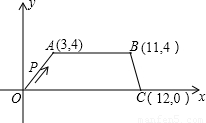
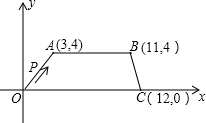 直角坐标系中O是原点,梯形OABC各顶点的坐标如图所示,
直角坐标系中O是原点,梯形OABC各顶点的坐标如图所示,查看答案和解析>>
科目:初中数学 来源:2012届山东省济南市辛锐中学九年级下学期模拟考试数学卷(带解析) 题型:解答题
如图,在直角坐标系中, 是原点,
是原点, 三点的坐标分别
三点的坐标分别 ,四边形
,四边形 是梯形,点
是梯形,点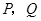 同时从原点出发,分别作匀速运动,其中点
同时从原点出发,分别作匀速运动,其中点 沿
沿 向终点
向终点 运动,速度为每秒
运动,速度为每秒 个单位,点
个单位,点 沿
沿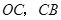 向终点
向终点 运动,当这两点有一点到达自己的终点时,另一点也停止运动.
运动,当这两点有一点到达自己的终点时,另一点也停止运动.
(1)求直线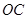 的解析式.
的解析式.
(2)设从出发起,运动了 秒.如果点
秒.如果点 的速度为每秒
的速度为每秒 个单位,试写出点
个单位,试写出点 的坐标,并写出此时
的坐标,并写出此时 的取值范围.
的取值范围.
(3)设从出发起,运动了 秒.当
秒.当 ,
, 两点运动的路程之和恰好等于梯形
两点运动的路程之和恰好等于梯形 的周长的一半,这时,直线
的周长的一半,这时,直线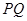 能否把梯形的面积也分成相等的两部分,如有可能,请求出
能否把梯形的面积也分成相等的两部分,如有可能,请求出 的值;如不可能,请说明理由.
的值;如不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2012届山东济南辛寨乡辛锐中学九年级下学业水平模拟考试数学卷(带解析) 题型:解答题
如图,在直角坐标系中,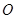 是原点,
是原点,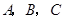 三点的坐标分别
三点的坐标分别 ,四边形
,四边形 是梯形,点
是梯形,点 同时从原点出发,分别作匀速运动,其中点
同时从原点出发,分别作匀速运动,其中点 沿
沿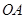 向终点
向终点 运动,速度为每秒
运动,速度为每秒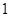 个单位,点
个单位,点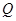 沿
沿 向终点
向终点 运动,当这两点有一点到达自己的终点时,另一点也停止运动.
运动,当这两点有一点到达自己的终点时,另一点也停止运动.
【小题1】求直线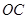 的解析式.
的解析式.
【小题2】设从出发起,运动了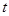 秒.如果点
秒.如果点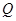 的速度为每秒
的速度为每秒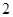 个单位,试写出点
个单位,试写出点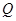 的坐标,并写出此时
的坐标,并写出此时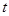 的取值范围.
的取值范围.
【小题3】设从出发起,运动了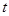 秒.当
秒.当 ,
,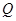 两点运动的路程之和恰好等于梯形
两点运动的路程之和恰好等于梯形 的周长的一半,这时,直线
的周长的一半,这时,直线 能否把梯形的面积也分成相等的两部分,如有可能,请求出
能否把梯形的面积也分成相等的两部分,如有可能,请求出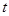 的值;如不可能,请说明理由.
的值;如不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年山东省济南市九年级下学期模拟考试数学卷(解析版) 题型:解答题
如图,在直角坐标系中,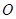 是原点,
是原点,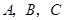 三点的坐标分别
三点的坐标分别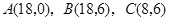 ,四边形
,四边形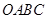 是梯形,点
是梯形,点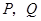 同时从原点出发,分别作匀速运动,其中点
同时从原点出发,分别作匀速运动,其中点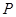 沿
沿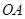 向终点
向终点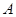 运动,速度为每秒
运动,速度为每秒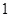 个单位,点
个单位,点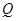 沿
沿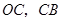 向终点
向终点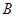 运动,当这两点有一点到达自己的终点时,另一点也停止运动.
运动,当这两点有一点到达自己的终点时,另一点也停止运动.

(1)求直线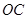 的解析式.
的解析式.
(2)设从出发起,运动了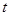 秒.如果点
秒.如果点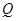 的速度为每秒
的速度为每秒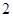 个单位,试写出点
个单位,试写出点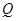 的坐标,并写出此时
的坐标,并写出此时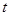 的取值范围.
的取值范围.
(3)设从出发起,运动了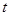 秒.当
秒.当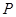 ,
,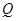 两点运动的路程之和恰好等于梯形
两点运动的路程之和恰好等于梯形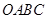 的周长的一半,这时,直线
的周长的一半,这时,直线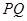 能否把梯形的面积也分成相等的两部分,如有可能,请求出
能否把梯形的面积也分成相等的两部分,如有可能,请求出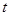 的值;如不可能,请说明理由.
的值;如不可能,请说明理由.
【解析】(1)根据待定系数法就可以求出直线OC的解析式(2)本题应分Q在OC上,和在CB上两种情况进行讨论.即0≤t≤5和5<t≤10两种情况(3)P、Q两点运动的路程之和可以用t表示出来,梯形OABC的周长就可以求得.当P、Q两点运动的路程之和恰好等于梯形OABC的周长的一半,就可以得到一个关于t的方程,可以解出t的值.梯形OABC的面积可以求出,梯形OCQP的面积可以用t表示出来.把t代入可以进行检验
查看答案和解析>>
科目:初中数学 来源:2011-2012学年山东济南辛寨乡辛锐中学九年级下学业水平模拟考试数学卷(解析版) 题型:解答题
如图,在直角坐标系中, 是原点,
是原点,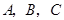 三点的坐标分别
三点的坐标分别
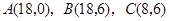 ,四边形
,四边形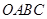 是梯形,点
是梯形,点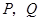 同时从原点出发,分别作匀速运动,其中点
同时从原点出发,分别作匀速运动,其中点 沿
沿 向终点
向终点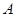 运动,速度为每秒
运动,速度为每秒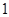 个单位,点
个单位,点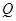 沿
沿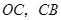 向终点
向终点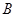 运动,当这两点有一点到达自己的终点时,另一点也停止运动.
运动,当这两点有一点到达自己的终点时,另一点也停止运动.
1.求直线 的解析式.
的解析式.
2.设从出发起,运动了 秒.如果点
秒.如果点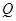 的速度为每秒
的速度为每秒 个单位,试写出点
个单位,试写出点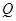 的坐标,并写出此时
的坐标,并写出此时 的取值范围.
的取值范围.
3.设从出发起,运动了 秒.当
秒.当 ,
,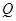 两点运动的路程之和恰好等于梯形
两点运动的路程之和恰好等于梯形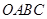 的周长的一半,这时,直线
的周长的一半,这时,直线 能否把梯形的面积也分成相等的两部分,如有可能,请求出
能否把梯形的面积也分成相等的两部分,如有可能,请求出 的值;如不可能,请说明理由.
的值;如不可能,请说明理由.
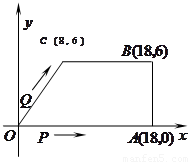
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com