
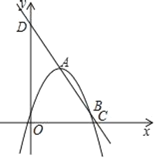
【题目】如图所示,二次函数y=k(x﹣1)2+2的图象与一次函数y=kx﹣k+2的图象交于A、B两点,点B在点A的右侧,直线AB分别与x、y轴交于C、D两点,其中k<0.
(1)求A、B两点的横坐标;
(2)若△OAB是以OA为腰的等腰三角形,求k的值;
(3)二次函数图象的对称轴与x轴交于点E,是否存在实数k,使得∠ODC=2∠BEC,若存在,求出k的值;若不存在,说明理由.
【答案】(1)1,2;(2)﹣1或﹣2或﹣3;(3)存在,![]() 或
或![]() .
.
【解析】
(1)将二次函数与一次函数联立得:k(x﹣1)2+2=kx﹣k+2,然后求解进一步得出答案即可;
(2)分两种情况:①OA=AB;②OA=OB,据此分类讨论即可;
(3)分两种情况:①当点B在x轴上方时;②当点B在x轴下方时,据此分类讨论即可.
解:(1)将二次函数与一次函数联立得:k(x﹣1)2+2=kx﹣k+2,
解得:x=1或2,
故点A、B的坐标横坐标分别为1和2;
(2)OA=![]() ,
,
①当OA=AB时,
即:1+k2=5,解得:k=±2(舍去2);
②当OA=OB时,
4+(k+2)2=5,解得:k=﹣1或﹣3;
故k的值为:﹣1或﹣2或﹣3;
(3)存在,理由:
①当点B在x轴上方时,
过点B作BH⊥AE于点H,将△AHB的图形放大见右侧图形,
过点A作∠HAB的角平分线交BH于点M,过点M作MN⊥AB于点N,过点B作BK⊥x轴于点K,
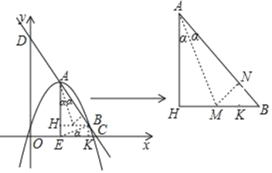
图中:点A(1,2)、点B(2,k+2),则AH=﹣k,HB=1,
设: HM=m=MN,则BM=1﹣m,
则AN=AH=﹣k,AB=![]() ,NB=AB﹣AN,
,NB=AB﹣AN,
由勾股定理得:MB2=NB2+MN2,
即:(1﹣m)2=m2+(![]() +k)2,
+k)2,
解得:m=﹣k2﹣k![]() ,
,
在△AHM中,tanα=![]() =
=![]() =k+
=k+![]() =tan∠BEC=
=tan∠BEC=![]() =k+2,
=k+2,
解得:k=![]() ,
,
此时k+2>0,则﹣2<k<0,故:舍去正值,
故k=﹣![]() ;
;
②当点B在x轴下方时,
同理可得:tanα=![]() =
=![]() =k+
=k+![]() =tan∠BEC=
=tan∠BEC=![]() ==-(k+2),
==-(k+2),
解得:k=![]() 或
或![]() ,
,
此时k+2<0,k<﹣2,故舍去![]() ,
,
故k的值为:﹣![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
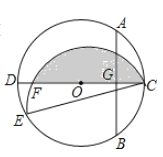
【题目】如图,CD是⊙O的直径,AB是⊙O的弦,AB⊥CD,垂足为G,OG:OC=3:5,AB=8.点E为圆上一点,∠ECD=15°,将![]() 沿弦CE翻折,交CD于点F,图中阴影部分的面积=_________
沿弦CE翻折,交CD于点F,图中阴影部分的面积=_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加快“智慧校园”建设,某市准备为试点学校采购一批![]() 两种型号的一体机,经过市场调查发现,每套
两种型号的一体机,经过市场调查发现,每套![]() 型一体机的价格比每套
型一体机的价格比每套![]() 型一体机的价格多
型一体机的价格多![]() 万元,且用
万元,且用![]() 万元恰好能购买
万元恰好能购买![]() 套
套![]() 型一体机和
型一体机和![]() 套
套![]() 型一体机.
型一体机.
(1)列二元一次方程组解决问题:求每套![]() 型和
型和![]() 型一体机的价格各是多少万元?
型一体机的价格各是多少万元?
(2)由于需要,决定再次采购![]() 型和
型和![]() 型一体机共
型一体机共![]() 套,此时每套
套,此时每套![]() 型体机的价格比原来上涨
型体机的价格比原来上涨![]() ,每套
,每套![]() 型一体机的价格不变.设再次采购
型一体机的价格不变.设再次采购![]() 型一体机
型一体机![]() 套,那么该市至少还需要投入多少万元?
套,那么该市至少还需要投入多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
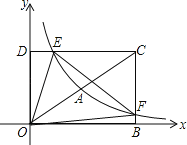
【题目】如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数![]() (x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y2=k2x+b.
(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y2=k2x+b.
(1)求反比例函数和直线EF的解析式;
(温馨提示:平面上有任意两点M(x1,y1)、N(x2,y2),它们连线的中点P的坐标为( ![]() ))(2)求△OEF的面积;
))(2)求△OEF的面积;
(3)请结合图象直接写出不等式k2x -b﹣![]() >0的解集.
>0的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
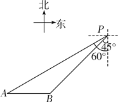
【题目】如图,一艘轮船位于灯塔P南偏西60°方向的A处,它向东航行20海里到达灯塔P南偏西45°方向上的B处,若轮船继续沿正东方向航行,求轮船航行途中与灯塔P的最短距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C三个城市位置如图所示,A城在B城正南方向180 km处,C城在B城南偏东37°方向.已知一列货车从A城出发匀速驶往B城,同时一辆客车从B城出发匀速驶往C城,出发1小时后,货车到达P地,客车到达M地,此时测得∠BPM=26°,两车又继续行驶1小时,货车到达Q地,客车到达N地,此时测得∠BNQ=45°,求两车的速度.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin26°≈
,sin26°≈![]() ,cos26°≈
,cos26°≈![]() ,tan26°≈
,tan26°≈![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
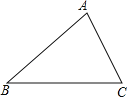
【题目】如图,锐角三角形ABC中,BC>AB>AC,甲、乙两人想找一点P,使得∠BPC与∠A互补,其作法分别如下:
(甲)以A为圆心,AC长为半径画弧交AB于P点,则P即为所求;
(乙)作过B点且与AB垂直的直线l,作过C点且与AC垂直的直线,交l于P点,则P即为所求.
对于甲、乙两人的作法,下列叙述何者正确?( )
A. 两人皆正确 B. 两人皆错误
C. 甲正确,乙错误 D. 甲错误,乙正确
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com