
����Ŀ��С���ҵ��ſ���װ��һ�ѷ�����������ͼ1������ƽ��ṹͼ��ͼ2��ʾ���������Կ����������Ȼ�AD����BC�;���ABCD��ɣ���BC��Բ���ǵ�����ť��M����֪��AD�Ĺ��θ�GH��2cm��AD��8cm��EP��11cm��������PN���ŵ�N��ת��NQλ��ʱ����������ʱֱ��PQ�뻡BC���ڵ�Բ���У���PQ��DN��tan��NQP��2��
��1����BC����Բ�İ뾶Ϊ_____cm��
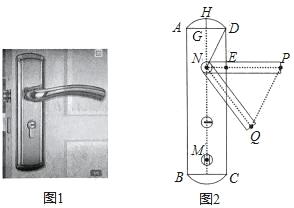
��2���߶�AB�ij���ԼΪ_____cm����![]() ��2.236�������ȷ��0.1cm��
��2.236�������ȷ��0.1cm��
���𰸡�5 29.8
��������
��1����ͼ������BM����HM��BC��K���ӳ�PQ��NM���ӳ����ڵ�T����ֱ��PQ�뻡BC���ڵ�Բ������J������MJ����Rt��BMK�����ù��ɶ�����һ�����ɣ�
��2����������ɽ�һ���ó�tan��DNE��tan��NQP��2��![]() ���Ӷ��ó�NP�ij������������tan��TMJ��tan��NPT��һ����⣬ͨ��GN+MN+MK���AB�ij�����.
���Ӷ��ó�NP�ij������������tan��TMJ��tan��NPT��һ����⣬ͨ��GN+MN+MK���AB�ij�����.
��ͼ������BM����HM��BC��K���ӳ�PQ��NM���ӳ����ڵ�T����ֱ��PQ�뻡BC���ڵ�Բ������J������MJ��

��BM��r����Rt��BMK������r2��42+��r��2��2��
���r��5��
��BM��5������BC����Բ�İ뾶Ϊ5cm��
��2����DN��PB��
���DNE����P��
��NP��NQ��
���P����NQP��
���DNE����NQP��
��tan��DNE��tan��NQP��2��![]() ��
��
��NE��DG��4��
��DE��NG��8��
��NP��NE+EP��4+11��15��
��ֱ��PQ�뻡BC���ڵ�Բ������J��
��MJ��PQ��MJ��5��
���TMJ����NPT��
��tan��TMJ��tan��NPT��2��
��![]() ��
��
��NT��15��2��30��TJ��5��2��10��
��MT=![]() ,
,
��MN��NT��MT��30��5![]() ��
��
��AB��GN+MN+MK��8+30��5![]() +3��41��5
+3��41��5![]() ��29.8cm
��29.8cm
�ʴ�Ϊ����1��5����2��29.8��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�ڽ��ڡ�O����I����ABC�����ģ���AIC=124������E��AD���ӳ����ϣ����CDE�Ķ���Ϊ��������
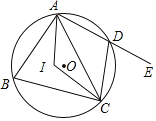
A. 56�� B. 62�� C. 68�� D. 78��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����عذ�����ѧ����ijѧУ������ѧ���ĸ������ηֳ��������ͣ�A���ɸ�ĸһ���տ���B����үү�����տ���C�������̵Ƚ����տ���D��ֱ�Ӽ���ѧУ��ij��ѧС�����������һ���༶�����ָð�����ѧ������ռȫ����������20%�������������Ƴ�����������������ͳ��ͼ��
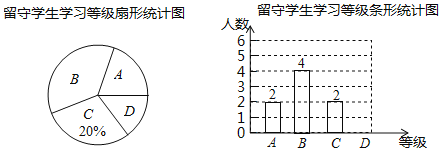
��1���ð���� ��������ѧ����B��������ѧ���������ε�Բ�ĽǵĶ���Ϊ�� ����
��2��������ͳ��ͼ����������
��3����֪��У����2400��ѧ������ѧУ�����D���͵�����ѧ�����������ֹذ����������Ƹ�У���ж���������ѧ���ڴ˹ذ�������棿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��C���߶�AB��һ�㣬AC��5cm����P�ӵ�A������AB��3cm/s���ٶ����B�˶�����Q�ӵ�C������CB��1cm/s���ٶ����B�˶�������ͬʱ�����������P�ȵ�Q�ȵ�3s��
��1����AB�ij���
��2�����P��Q������ʱ��Ϊts�����Pû�г�����Qʱ��t��ȡֵ��Χ��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪x2��8x+16��m2��0��m��0���ǹ���x��һԪ���η���
��1��֤�����˷���������������ȵ�ʵ������
��2����������ABC��һ�߳�a��6�������߳�b��c�Ǹ÷��̵�����ʵ����������ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2015��������װ������һ���ﶬ������������1.2�ף�����0.8�ף���֪���ϵĵ��۱����ϵĵ��۵�2������10Ԫ��һ�����IJ��ϳɱ�Ϊ76Ԫ��
��1�������Ϻ����ϵĵ��ۣ�
��2���ÿ�����9�·�Ͷ���г���������Ϊ150Ԫ/�������ֹ�������̬�ƣ�10�·ݽ�����������������������ȡ���۴�������֪����һ���������˹��ȹ̶�����14Ԫ��Ϊȷ��ÿ������������30Ԫ��
����10�·ݳ����Ĵ�����Ϊm����m����Сֵ��������=���ۼ۩����ϳɱ����̶����ã�
�ڽ���11�·��Ժ�����������ֺ�ת������������VIP�ͻ���10�·�����ۿۼ۵Ļ�����ʵʩ������Żݣ�����ͨ�ͻ���10�·�����ۿۼ۵Ļ�����ʵʩ�۸��ϸ�����֪��VIP�ͻ��Ľ����ʺͶ���ͨ�ͻ����������ȣ����һ��VIP�ͻ���9120Ԫ�������ļ�����һ����ͨ�ͻ���10080Ԫ�������ļ�����ͬ����VIP�ͻ����ܵĽ����ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABC�ڽ��ڡ�O������CO���ӳ���AB�ڵ�E������O�ڵ�D�������BEC��3��ACD��
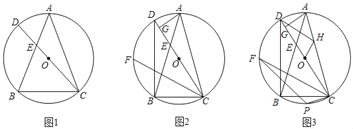
��1����ͼ1����֤��AB��AC��
��2����ͼ2������BD����FΪ��BD��һ�㣬����CF����CF����BD������A��AG��CD������Ϊ��G����֤��CF+DG��CG��
��3����ͼ3���ڣ�2���������£���HΪAC��һ�㣬�ֱ�����DH��OH��OH��DH������C��CP��AC������O�ڵ�P��OH��CP��1��![]() ��CF��12������PF����PF�ij���
��CF��12������PF����PF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����OAP�ǵ���ֱ�������Σ���OAP��90������A�ڵ������ޣ���P����Ϊ��8��0����������y��ax2+bx+c����ԭ��O��A��P���㣮
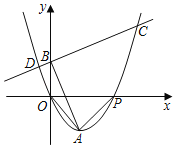
��1���������ߵĺ�����ϵʽ��
��2����B��y����������һ�㣬����AB������B��AB�Ĵ��߽���������C��D���㣬��BC��AB�����B���ꣻ
��3���ڣ�2���������£���M���߶�BC��һ�㣬����M��x��Ĵ��߽��������ڵ�N�����CBN��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼʾ������ABC��һ��P������PAC=��PBA=��PCB�����PΪ��ABC�IJ��忨�㣮�����εIJ��忨�㣨Brocard point���Ƿ�����ѧ�Һ���ѧ�����ҿ������A��L��Crelle 1780��1855����1816���״η��֣������ķ��ֲ�δ����ʱ��������ע�⣬1875�꣬���忨�㱻һ����ѧ�����߷������ٲ��忨��Brocard 1845��1922�����·��֣����������������������⣺��֪�ڵ���ֱ��������DEF�У���EDF=90�㣬����QΪ��DEF�IJ��忨�㣬DQ=1����EQ+FQ=�� ��
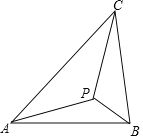
A��5 B��4 C��3+![]() D��2+
D��2+![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com