
【题目】如图,已知![]() ,
,![]() ,点
,点![]() 是射线
是射线![]() 上一动点(与点
上一动点(与点![]() 不重合),
不重合),![]() 分别平分
分别平分![]() 和
和![]() ,分别交射线
,分别交射线![]() 于点
于点![]() .
.

(1)![]() ;
;![]() ;
;
(2)当点![]() 运动到某处时,
运动到某处时,![]() ,求此时
,求此时![]() 的度数.
的度数.
(3)当点![]() 运动时,
运动时,![]() :
:![]() 的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律;
的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律;
【答案】(1)100°,50°;(2)25°;(3)∠APB:∠ADB=2:1.
【解析】
(1)由平行线的性质:两直线平行同旁内角互补可得![]() 100°;再根据角平分线的定义可得2∠CBP+2∠DBP=100°,即可得
100°;再根据角平分线的定义可得2∠CBP+2∠DBP=100°,即可得![]() 50°.
50°.
(2)由平行可得∠ACB=∠CBN,结合已知![]() 可得∠ABC=∠CBP=∠DBP=∠DBN即可解决问题;即
可得∠ABC=∠CBP=∠DBP=∠DBN即可解决问题;即![]() =
=![]() =25°.
=25°.
(3)可以证明∠APB=∠PBN,∠ADB=∠DBN=![]() ∠PBN.
∠PBN.
解:(1)∵AM∥BN,∠A=80°,
∴∠A+∠ABN=180°,
∴∠ABN=100°;
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP,∠PBN=2∠DBP,
∴2∠CBP+2∠DBP=100°,
∴∠CBD=∠CBP+∠DBP=50°;
故答案为:100°,50°;
(2)∵AM∥BN,
∴∠ACB=∠CBN,
又∵∠ACB=∠ABD,
∴∠CBN=∠ABD,
∴∠ABC=∠ABD-∠CBD=∠CBN-∠CBD=∠DBN,
∴∠ABC=∠CBP=∠DBP=∠DBN,
∴∠ABC=![]() ∠ABN=
∠ABN=![]() =25°,
=25°,
(3)不变.理由如下:
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
又∵BD平分∠PBN,
∴∠ADB=∠DBN=![]() ∠PBN=
∠PBN=![]() ∠APB,
∠APB,
即∠APB:∠ADB=2:1.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:
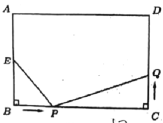
【题目】如图,在长方形ABCD中,AB=8cm,BC=12cm,点E为AB中点,如果点P在线段BC上以每秒4cm的速度,由点B向点C运动,同时,点Q在线段CD上以v厘米/秒的速度,由点C向点D运动,设运动时间为t秒.
(1)直接写出:PC= 厘米,CQ= 厘米;(用含t、v的代数式表示)
(2)若以E、B、P为顶点的三角形和以P、C、Q为顶点的三角形全等,试求v、t的值;
(3)若点Q以(2)中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针方向沿长方形ABCD的四边运动,求经过多长时间点P与点Q第一次在长方形ABCD的哪条边上相遇?
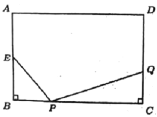
备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】供电局的电力维修工甲、乙两人要到30千米远的A地进行电力抢修.甲骑摩托车先行,![]() 小时后乙开抢修车载着所需材料出发,结果甲、乙两人同时到达.已知抢修车的速度是摩托车的1.5倍,求摩托车的速度.
小时后乙开抢修车载着所需材料出发,结果甲、乙两人同时到达.已知抢修车的速度是摩托车的1.5倍,求摩托车的速度.
(1)设摩托车的速度为x千米/时,利用速度、时间、路程之间的关系填写下表.
(要求:填上适当的代数式,完成表格)
速度(千米/时) | 所走的路程(千米) | 所用时间(时) | |
摩托车 | x | 30 | |
抢修车 | 30 |
(2)列出方程,并求摩托车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
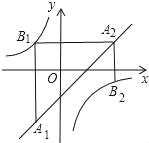
【题目】如图,已知点A1,A2,…,An均在直线y=x﹣2上,点B1,B2,…,Bn均在双曲线y=﹣![]() 上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=﹣2,则a2016=_____.
上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=﹣2,则a2016=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣3、﹣2、﹣1、1、2、3六个数中任选一个数记为k,若数k使得关于x的分式方程![]() =k﹣2有解,且使关于x的一次函数y=(k+
=k﹣2有解,且使关于x的一次函数y=(k+![]() )x+2不经过第四象限,那么这6个数中,所有满足条件的k的值之和是( )
)x+2不经过第四象限,那么这6个数中,所有满足条件的k的值之和是( )
A. ﹣1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a、b、c为△ABC的三边。
(1)判断代数式a![]() 2abc
2abc![]() +b
+b![]() 的值与0的大小关系,并说明理由;
的值与0的大小关系,并说明理由;
(2)满足a![]() +b
+b![]() +c
+c![]() =ab+ac+bc,试判断△ABC的形状.
=ab+ac+bc,试判断△ABC的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
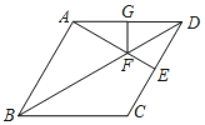
【题目】如图,在菱形ABCD中,∠ABC=60°,过点A作AE⊥CD于点E,交对角线BD于点F,过点F作FG⊥AD于点G.
(1)若AB=2,求四边形ABFG的面积;
(2)求证:BF=AE+FG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,BG=4![]() ,则△EFC的周长为( )
,则△EFC的周长为( )
A. 11 B. 10 C. 9 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1所示的三棱柱,高为![]() ,底面是一个边长为
,底面是一个边长为![]() 的等边三角形.
的等边三角形.
(1)这个三棱柱有 条棱,有 个面;
(2)图2方框中的图形是该三棱柱的表面展开图的一部分,请将它补全;
(3)要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,需剪开 条棱,需剪开棱的棱长的和的最大值为 ![]() .
.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com