
分析 根据a是33立方根,$\sqrt{{4}^{2}}$的平方根是b,可以求得a、b的值,从而可以求得$\sqrt{a+b}$的值.
解答 解:∵a是33的立方根,$\sqrt{{4}^{2}}$的平方根是b,
∴a=$\root{3}{{3}^{3}}=3$,b=$±\sqrt{\sqrt{{4}^{2}}}=±\sqrt{4}=±2$,
∴当a=3,b=2时,$\sqrt{a+b}=\sqrt{3+2}=\sqrt{5}$,
当a=3,b=-2时,$\sqrt{a+b}=\sqrt{3+(-2)}=1$,
故答案为:$\sqrt{5}$或1.
点评 本题考查立方根、平方很、算术平方根,解答本题的关键它们各自的含义.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
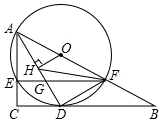 如图,在Rt△ABC中,∠C=90°,点O在AB上,经过点A的⊙O与BC相切于点D,与AC,AB分别相交于点E,F,连接AD与EF相交于点G.
如图,在Rt△ABC中,∠C=90°,点O在AB上,经过点A的⊙O与BC相切于点D,与AC,AB分别相交于点E,F,连接AD与EF相交于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,竹条AB的长为25cm,贴纸部分的宽BD为15cm,若纸扇两面贴纸,则一面贴纸的面积为175πcm2(结果保留π).
如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,竹条AB的长为25cm,贴纸部分的宽BD为15cm,若纸扇两面贴纸,则一面贴纸的面积为175πcm2(结果保留π).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
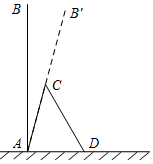 一棵大树AB(假定大树AB垂直于地面)被刮倾斜15°后折断在地上,树的顶部恰好接触到地面D处(如示意图所示),量得大树的倾斜角∠BAC=15°,大树被折断部分和地面所成的角∠ADC=60°,AD=4米,求大树AB原来的高度是多少米?(结果保留整数,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4)
一棵大树AB(假定大树AB垂直于地面)被刮倾斜15°后折断在地上,树的顶部恰好接触到地面D处(如示意图所示),量得大树的倾斜角∠BAC=15°,大树被折断部分和地面所成的角∠ADC=60°,AD=4米,求大树AB原来的高度是多少米?(结果保留整数,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
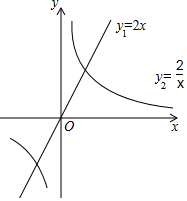 在平面直角坐标系xOy中,直线y1=2x与双曲线y2=$\frac{2}{x}$ 的图象如图所示,小明说:“满足y1>y2的x的取值范围是x>1.”你同意他的观点吗?答:不同意.理由是y1>y2的x的取值范围是x>1或-1<x<0.
在平面直角坐标系xOy中,直线y1=2x与双曲线y2=$\frac{2}{x}$ 的图象如图所示,小明说:“满足y1>y2的x的取值范围是x>1.”你同意他的观点吗?答:不同意.理由是y1>y2的x的取值范围是x>1或-1<x<0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com