1.阅读下面材料:
根据乘方的意义填空:
(1)①${2}^{2}×{2}^{3}=\underset{\underbrace{2×2}}{2个}\underset{\underbrace{×2×2×2}}{3个}=\underset{\underbrace{2×2×2×2×2}}{(2+3)个}={2}^{5}={2}^{(2+3)}$
一般地,${a}^{m}×{a}^{n}=\underset{\underbrace{a•a•a•…•a•}}{m个}\underset{\underbrace{a•a•a•…•a}}{n\;个}=\underset{\underbrace{a•a•a•…•a}}{(\;\;\;\;\;\;\;\;\;)个}={a}^{(\;\;\;\;\;\;)}$
②$({2}^{2})^{3}=\underset{\underbrace{{2}^{2}×{2}^{2}×{2}^{2}}}{3个}=\underset{\underbrace{(2×2)×(2×2)×(2×2)}}{3个}=\underset{\underbrace{2×2×2×2×2×2}}{2×3个}={2}^{6}={2}^{2×3}$
一般地,
$({a}^{m})^{n}=\underset{\underbrace{{a}^{m}•{a}^{m}•{a}^{m}•…•{a}^{m}}}{n个}=\underset{\underbrace{\underset{\underbrace{(a•a•a•…•a)}}{m个}\underset{\underbrace{(a•a•a•…•a)}}{m个}\underset{\underbrace{(a•a•a•…•a)•}}{m个}\underset{…\underbrace{•(a•a•a•…•a)}}{m个}}}{n个}{=\underset{\underbrace{a•a•a•…•a}}{(\;\;\;\;\;\;\;\;)个}=a}^{(\;\;\;\;\;\;)}$③${2}^{3}×(\frac{1}{2})^{3}=\underset{\underbrace{2×2×2}}{3个}\underset{×\underbrace{\frac{1}{2}×\frac{1}{2}×\frac{1}{2}}}{3个}=\underset{\underbrace{(2×\frac{1}{2})×(2×\frac{1}{2})×(2×\frac{1}{2})}}{3个}=(2×\frac{1}{2})^{3}$
一般地,${a}^{m}•{a}^{n}=\underset{\underbrace{(a•a•a•…•a)}}{m个}\underset{\underbrace{(b•b•b•…•b)}}{m个}=\underset{\underbrace{(ab)•(ab)•(ab)•…•(ab)}}{(\;\;\;\;\;\;\;\;\;\;\;)个}=(ab)^{(\;\;\;\;\;)}$
(2)根据上面的知识,计算:
①(-5)4×(-5)6
②${[{{{(-\frac{1}{2})}^4}}]^3}$
③(-0.125)99×8100.
分析 (2)①根据同底数幂的乘法法则计算即可求解;
②根据幂的乘方法则计算即可求解;
③逆用积的乘方法则计算即可求解.
解答 解:(2)①(-5)4×(-5)6=(-5)10=510;
②${[{{{(-\frac{1}{2})}^4}}]^3}$=(-$\frac{1}{2}$)12=($\frac{1}{2}$)12;
③(-0.125)99×8100=(-0.125×8)99×8=-8.
点评 考查了整式的混合运算,关键是熟练掌握同底数幂的乘法,幂的乘方和积的乘方的知识点.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案
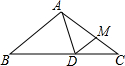 如图,在△ABC中,AB=AC=10,BC=16,D和M分别是BC、AC边上的动点,则AD+DM的最小值是$\frac{48}{5}$.
如图,在△ABC中,AB=AC=10,BC=16,D和M分别是BC、AC边上的动点,则AD+DM的最小值是$\frac{48}{5}$.