
【题目】如图,若把边长为1的正方形ABCD的四个角(阴影部分)剪掉,得一四边形A1B1C1D1 . 试问怎样剪,才能使剩下的图形仍为正方形,且剩下图形的面积为原来正方形面积的 ![]() ,请说明理由.(写出证明及计算过程)
,请说明理由.(写出证明及计算过程) 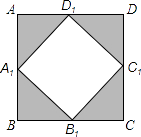
【答案】解:∵A1B1C1D1是正方形, ∴A1B1=B1C1=C1D1=D1A1 ,
∵∠AA1D1+∠AD1A1=90°,∠AA1D1+∠BA1B1=90°,
∴∠AD1A1=∠BA1B1 ,
同理可得:∠AD1A1=∠BA1B1=∠DC1D1=∠C1B1C,
∵∠A=∠B=∠C=∠D,
∴△AA1D1≌△BB1A1≌△CC1B1≌△DD1C1 ,
∴AA1=D1D,
设AD1=x,那么AA1=DD1=1﹣x,
Rt△AA1D1中,根据勾股定理可得:
A1D12=x2+(1﹣x)2 ,
∴正方形A1B1C1D1的面积=A1D12=x2+(1﹣x)2= ![]() ,
,
解得x= ![]() ,x=
,x= ![]() .
.
答:依次将四周的直角边分别为 ![]() 和
和 ![]() 的直角三角形减去即可.
的直角三角形减去即可.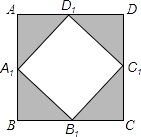
【解析】本题中易证四边的四个小直角三角形全等,那么可设一边为x,那么另一边就是(1﹣x),可用勾股定理求出里面的正方形的边长的平方也就是其面积,然后根据剩下图形的面积为原来正方形面积的 ![]() ,来列方程求解.
,来列方程求解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(12分)在上学期的几次测试中,小张和小王的几次数学成绩(单位:分)如下表:

两人都说自己的数学成绩更好.请你想一想:
(1)小张可能是根据什么来判断的?小王可能是根据什么来判断的?
(2)你能根据小张的想法设计一种方案使小张的成绩比小王的高吗?写出你的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线BC于点M,切点为N,则DM的长为( ) 
A.![]()
B.![]()
C.![]()
![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若AB=2BC,∠F=36°,求∠B的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E,F是对角线AC上的两点,且AE=CF.下列结论:①BE=DF;②BE∥DF;③AB=DE;④四边形EBFD为平行四边形;⑤S△ADE=S△ABE;⑥AF=CE.其中正确的个数是( )

A. 3个 B. 4个 C. 5个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(0,a),B(b,a),且a、b满足(a﹣2)2+|b﹣4|=0,现同时将点A,B分别向下平移2个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.

(1)求点C,D的坐标及四边形ABDC的面积S四边形ABCD;
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=![]() S四边形ABDC?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
S四边形ABDC?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
(3)点P是直线BD上的一个动点,连接PA,PO,当点P在BD上移动时(不与B,D重合),直接写出∠BAP、∠DOP、∠APO之间满足的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
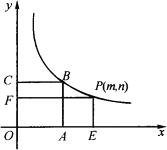
【题目】如图,正方形OABC的面积为9,点O为左边原点,点A在![]() 轴上,点C在
轴上,点C在![]() 轴上,点B在函数
轴上,点B在函数![]() 的图象上,点P
的图象上,点P![]() 是函数
是函数![]() 图象上的任意一点,过点P分别作
图象上的任意一点,过点P分别作![]() 轴、
轴、![]() 轴的垂线,垂足分别为E、F,并设矩形OEPF和正方形OABC不重合的部分(图中阴影部分)的面积为S.
轴的垂线,垂足分别为E、F,并设矩形OEPF和正方形OABC不重合的部分(图中阴影部分)的面积为S.
(1)求B点坐标和![]() 值;
值;
(2)当![]() 时,求P点坐标.
时,求P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平行四边形ABCD中,CE平分∠BCD且交AD于点E,A F∥CE,且交BC于点F.
(1)求证:△ABF≌△CDE;
(2)如图,若∠1=65°,求∠B的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一根木棒放在数轴上,数轴的1个单位长度为1 cm,木棒的左端点与数轴上的点A重合,右端点与点B重合.
(1)若将木棒沿数轴水平向右移动,则当它的左端点移动到点B处时,它的右端点在数轴上所对应的数为20;若将木棒沿数轴水平向左移动,则当它的右端点移动到点A处时,它的左端点在数轴上所对应的数为5,由此可得到木棒的长为________cm.
(2)图中点A表示的数是________,点B表示的数是________.
(3)根据(1)(2),请你借助“数轴”这个工具帮助小红解决下列问题:
一天,小红问爷爷的年龄,爷爷说:“我若是你现在这么大,你还要40年才出生;你若是我现在这么大,我已经125岁,是老寿星了,哈哈!”请求出爷爷现在多少岁了.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com