

���� ��1�����������ߵĽ���ʽȷ���Գ���Ϊֱ��x=2�������öԳ��Եõ�2-��m-2��=2m+3-2���ⷽ�̿ɵ�m��ֵ���Ӷ��õ�A��-1��0����B��5��0����Ȼ���A���������y=-$\frac{3}{5}$[��x-2��2+n]�����n��ֵ��
��2����ND��y�ύBC��D����ͼ2�����������߽���ʽȷ��C��0��3���������ô���ϵ�������ֱ��BC�Ľ���ʽΪy=-$\frac{3}{5}$x+3����N��x��-$\frac{3}{5}$x2+$\frac{12}{5}$x+3������D��x��-$\frac{3}{5}$x+3�������������������ʽ������S��NBC=S��NDC+S��NDB�ɵ�S��BCN=-$\frac{3}{2}$x2+$\frac{15}{2}$x��Ȼ�����ö��κ�����������⣻
��3�������ù��ɶ��������BC=$\sqrt{34}$���ٷ������ۣ�����PMB=90�㣬���PMC=90�㣬��PMCΪ����ֱ�������Σ�MP=MC����PM=t����CM=t��MB=$\sqrt{34}$-t��֤����BMP�ס�BOC���������Ʊȿ����BP�ij����ټ���OP��ɵõ�P�����ꣻ����MPB=90�㣬��MP=MC����PM=t����CM=t��MB=$\sqrt{34}$-t��֤����BMP�ס�BCO���������Ʊȿ����BP�ij����ټ���OP��ɵõ�P�����꣮
��� �⣺��1���������ߵĽ���ʽΪy=-$\frac{3}{5}$[��x-2��2+n]=-$\frac{3}{5}$��x-2��2-$\frac{3}{5}$n��
�������ߵĶԳ���Ϊֱ��x=2��
�ߵ�A�͵�BΪ�ԳƵ㣬
��2-��m-2��=2m+3-2�����m=1��
��A��-1��0����B��5��0����
��A��-1��0������y=-$\frac{3}{5}$[��x-2��2+n]��9+n=0�����n=-9��
��2��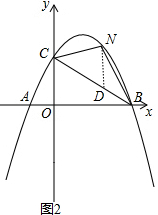 ��ND��y�ύBC��D����ͼ2��
��ND��y�ύBC��D����ͼ2��
�����߽���ʽΪy=-$\frac{3}{5}$[��x-2��2-9]=-$\frac{3}{5}$x2+$\frac{12}{5}$x+3��
��x=0ʱ��y=3����C��0��3����
��ֱ��BC�Ľ���ʽΪy=kx+b��
��B��5��0����C��0��3�������$\left\{\begin{array}{l}{5k+b=0}\\{b=3}\end{array}\right.$�����$\left\{\begin{array}{l}{k=-\frac{3}{5}}\\{b=3}\end{array}\right.$��
��ֱ��BC�Ľ���ʽΪy=-$\frac{3}{5}$x+3��
��N��x��-$\frac{3}{5}$x2+$\frac{12}{5}$x+3������D��x��-$\frac{3}{5}$x+3����
��ND=-$\frac{3}{5}$x2+$\frac{12}{5}$x+3-��-$\frac{3}{5}$x+3��=-$\frac{3}{5}$x2+3x��
��S��NBC=S��NDC+S��NDB=$\frac{1}{2}$•5•ND=-$\frac{3}{2}$x2+$\frac{15}{2}$x=-$\frac{3}{2}$��x-$\frac{5}{2}$��2+$\frac{75}{8}$��
��x=$\frac{5}{2}$ʱ����NBC���������ֵΪ$\frac{75}{8}$��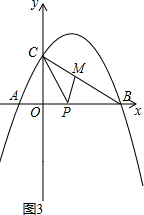
��3�����ڣ�
��B��5��0����C��0��3����
��BC=$\sqrt{{3}^{2}+{5}^{2}}$=$\sqrt{34}$��
����PMB=90�㣬���PMC=90�㣬��PMCΪ����ֱ�������Σ�MP=MC��
��PM=t����CM=t��MB=$\sqrt{34}$-t��
�ߡ�MBP=��OBC��
���BMP�ס�BOC��
��$\frac{PM}{OC}$=$\frac{BM}{OB}$=$\frac{BP}{BC}$����$\frac{t}{3}$=$\frac{\sqrt{34}-t}{5}$=$\frac{BP}{\sqrt{34}}$�����t=$\frac{3\sqrt{34}}{8}$��BP=$\frac{17}{4}$��
��OP=OB-BP=5-$\frac{17}{4}$=$\frac{3}{4}$��
��ʱP������Ϊ��$\frac{3}{4}$��0����
����MPB=90�㣬��MP=MC��
��PM=t����CM=t��MB=$\sqrt{34}$-t��
�ߡ�MBP=��CBO��
���BMP�ס�BCO��
��$\frac{MP}{OC}$=$\frac{BM}{BC}$=$\frac{BP}{BO}$����$\frac{t}{3}$=$\frac{\sqrt{34}-t}{\sqrt{34}}$=$\frac{BP}{5}$�����t=$\frac{102-9\sqrt{34}}{25}$��BP=$\frac{34-3\sqrt{34}}{5}$��
��OP=OB-BP=5-$\frac{34-3\sqrt{34}}{5}$=$\frac{3\sqrt{34}-9}{5}$��
��ʱP������Ϊ��$\frac{3\sqrt{34}-9}{5}$��0����
����������P��������$\frac{3\sqrt{34}-9}{5}$��0����$\frac{3}{4}$��0����
���� ���⿼���˶��κ������ۺ��⣺�������ն��κ���ͼ���ϵ�����������Ͷ��κ��������ʣ������ô���ϵ������������ʽ������������ͼ�ε����ʣ��������������ε��ж������������Ʊȼ����߶εij����ʾ�߶�֮��Ĺ�ϵ��ѧ�����÷������۵�˼������ѧ���⣮


 ʱ�����������ҵԭ���ܳ�����ϵ�д�
ʱ�����������ҵԭ���ܳ�����ϵ�д� ����νӽ̲���ĩ���Ԥϰ�人������ϵ�д�
����νӽ̲���ĩ���Ԥϰ�人������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{1}{6}$ | D�� | $\frac{1}{9}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��A�ص�B������һ����·���ù����ɼס������ӹ�ͬ��ɣ��ס������ӷֱ��A�ء�B��ͬʱ��ʼ��·������·��ʱ��Ϊx���죩��δ��·��Ϊy���ף���ͼ�е����߱�ʾ�����������̶Ӵӿ�ʼʩ�������̽����Ĺ�����y��x֮��ĺ�����ϵ����֪����·�����У����̶����豸������ͣ��5�죬���豸��������̶�ÿ����·��ԭ����533$\frac{1}{3}$�ף�
��A�ص�B������һ����·���ù����ɼס������ӹ�ͬ��ɣ��ס������ӷֱ��A�ء�B��ͬʱ��ʼ��·������·��ʱ��Ϊx���죩��δ��·��Ϊy���ף���ͼ�е����߱�ʾ�����������̶Ӵӿ�ʼʩ�������̽����Ĺ�����y��x֮��ĺ�����ϵ����֪����·�����У����̶����豸������ͣ��5�죬���豸��������̶�ÿ����·��ԭ����533$\frac{1}{3}$�ף��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com