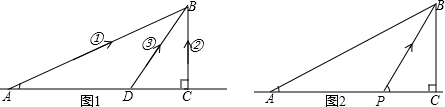
如图,海事救援指挥中心A接到海上SOS呼救:一艘渔船B在海上碰到暗礁,船体漏水下沉,5名船员需要援救.经测量渔船B到海岸最近的点C的距离BC=20km,∠BAC=22°37′,指挥中心立即制定三种救援方案(如图1):
①派一艘冲锋舟直接从A开往B;②先用汽车将冲锋舟沿海岸线送到点C,然后再派冲锋舟前往B;③先用汽车将冲锋舟沿海岸线送到距指挥中心33km的点D,然后再派冲锋舟前往B.
已知冲锋舟在海上航行的速度为60km/h,汽车在海岸线上行驶的速度为90km/h.
(sin22°37′=
,cos22°37′=
,tan22°37′=
)
(1)通过计算比较,这三种方案中,哪种方案较好(汽车装卸冲锋舟的时间忽略不计)?
(2)事后,细心的小明发现,上面的三种方案都不是最佳方案,最佳方案应是:先用汽车将冲锋舟沿海岸线送到点P处,点P满足cos∠BPC=
(冲锋舟与汽车速度的比),然后再派冲锋舟前往B(如图2).请你说明理由!
如果你反复探索没有解决问题,可以选取①、②、③两种研究方法:
方案①:在线段上AP任取一点M;然后用转化的思想,从几何的角度说明汽车行AM加上冲锋舟行BM的时间比车行AP加上冲锋舟行BP的时间要长.
方案②:在线段上AP任取一点M;设AM=x;然后用含有x的代数式表示出所用时间t;
方案③:利用现有数据,根据cos∠BPC=
计算出汽车行AP加上冲锋舟行BP的时间.

 -cos30°
-cos30°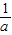 )
)