
【题目】某体育文化用品商店购进篮球和排球共200个,进价和售价如下表全部销售完后共获利润2600元.
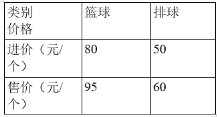
(1)求商店购进篮球和排球各多少个?
(2)王老师在元旦节这天到该体育文化用品商店为学校买篮球和排球各若干个(两种球都买了),商店在他的这笔交易中获利100元王老师有哪几种购买方案.
【答案】(1)商店购进篮球120个,排球80个;(2)王老师共有3种购买方案,方案1:购进篮球2个,排球7个;方案2:购进篮球4个,排球4个;方案3:购进篮球6个,排球1个
【解析】
(1)设商店购进篮球x个,排球y个,根据商店购进两种球共200个且销售利润为2600元,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设王老师购买篮球m个,排球n个,根据商店在他的这笔交易中获利100元,即可得出关于m,n的二元一次方程,结合m,n均为正整数,即可得出各购买方案.
解:(1)设商店购进篮球x个,排球y个,
依题意,得:![]() ,
,
解得:![]() ,
,
答:商店购进篮球120个,排球80个;
(2)设王老师购买篮球m个,排球n个,
依题意,得:(95﹣80)m+(60﹣50)n=100,
解得:n=10﹣![]() m,
m,
∵m,n均为正整数,
∴m为偶数,
∴当m=2时,n=7;当m=4时,n=4;当m=6时,n=1,
∴王老师共有3种购买方案,方案1:购进篮球2个,排球7个;方案2:购进篮球4个,排球4个;方案3:购进篮球6个,排球1个.


科目:初中数学 来源: 题型:
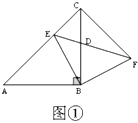
【题目】如图,已知![]() ,点
,点![]() 为直线
为直线![]() 上一点,以
上一点,以![]() 为边,点
为边,点![]() 为直角顶点作等腰直角三角形
为直角顶点作等腰直角三角形![]() .
.
(1)如图①,当点![]() 在线段
在线段![]() 上时,
上时,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ;
;
①找出一对全等三角形为_____________;
②若四边形![]() 的面积为7,则
的面积为7,则![]() 的长是_______.
的长是_______.
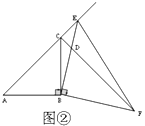
(2)如图②,当点![]() 在
在![]() 的延长线上时,
的延长线上时,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
①![]() 的面积记为
的面积记为![]() ,
,![]() 的面积记为
的面积记为![]() ,探究
,探究![]() 、
、![]() 之间的数量关系并说明理由;
之间的数量关系并说明理由;
②当![]() 的面积为1时,求
的面积为1时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标平面内,抛物线经过原点![]() 、点
、点![]() ,又与
,又与![]() 轴正半轴相交于点
轴正半轴相交于点![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上的一点,过点
上的一点,过点![]() 作
作![]() ,与抛物线交于点
,与抛物线交于点![]() ,且点
,且点![]() 在第一象限内.
在第一象限内.
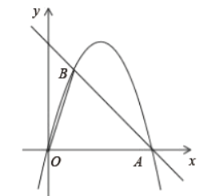
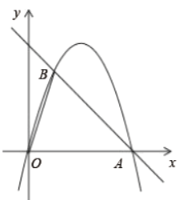
备用图
(1)求抛物线的表达式;
(2)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)过点![]() 作
作![]() 轴,分别交直线
轴,分别交直线![]() 、
、![]() 轴于点
轴于点![]() 、
、![]() ,若
,若![]() 的面积等于
的面积等于![]() 的面积的
的面积的![]() 倍,求
倍,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(﹣1,0)B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点.
(1)求抛物线的解析式和直线AC的解析式;
(2)请在y轴上找一点M,使△BDM的周长最小,求出点M的坐标;
(3)试探究:在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
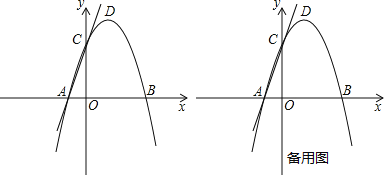
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中,![]() 是直角三角形,
是直角三角形,![]() ,点
,点![]() 、
、![]() 的横坐标是一元二次方程
的横坐标是一元二次方程![]() 的两根(
的两根(![]() ),直线
),直线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 点的坐标为
点的坐标为![]() .
.
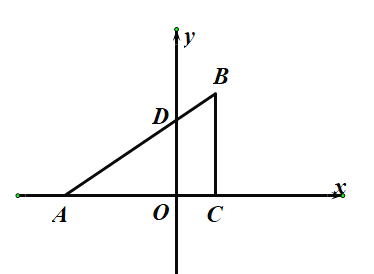
(1)求直线![]() 的函数表达式;
的函数表达式;
(2)在![]() 轴上找一点
轴上找一点![]() ,连接
,连接![]() ,使得以点
,使得以点![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似(不包括全等),并求点
相似(不包括全等),并求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,点![]() 、
、![]() 分别是
分别是![]() 和
和![]() 上的动点,连接
上的动点,连接![]() ,点
,点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,以每秒1个单位长度的速度运动,当点
同时出发,以每秒1个单位长度的速度运动,当点![]() 到达点
到达点![]() 时,两点停止运动,设运动时间为
时,两点停止运动,设运动时间为![]() 秒,请直接写出几秒时以点
秒,请直接写出几秒时以点![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似.
相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,…,其中从第三个数起,每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的边长值构造正方形,再分别依次从左到右取2个、3个、4个、5个…正方形拼成如上长方形,若按此规律继续作长方形,则序号为⑦的长方形周长是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AC是对角线,E是AD边上一点,连接BE交AC于点F,∠FAE=∠FEA=30°,G为AB边的中点,连接GF.
(1)如图1,若BC=![]() ,AF=2,求△AGF的面积;
,AF=2,求△AGF的面积;
(2)如图2,过点G作GH⊥GF,连接HA交BC于点M,连接HC,且HA=HC,连接HF,求证:MC=![]() MH
MH

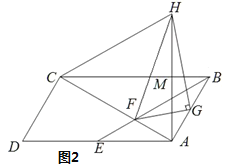
查看答案和解析>>
科目:初中数学 来源: 题型:
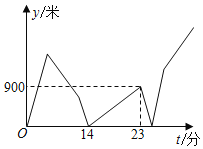
【题目】已知A、B、C三地顺次在同一直线上,甲、乙两人均骑车从A地出发,向C地匀速行驶.甲比乙早出发5分钟,甲到达B地并休息了2分钟后,乙追上了甲.甲、乙同时从B地以各自原速继续向C地行驶.当乙到达C地后,乙立即掉头并提速为原速的![]() 倍按原路返回A地,而甲也立即提速为原速的
倍按原路返回A地,而甲也立即提速为原速的![]() 倍继续向C地行驶,到达C地就停止.若甲、乙间的距离y(米)与甲出发的时间t(分)之间的函数关系如图所示,则当甲到达C地时,乙距A地_____米.
倍继续向C地行驶,到达C地就停止.若甲、乙间的距离y(米)与甲出发的时间t(分)之间的函数关系如图所示,则当甲到达C地时,乙距A地_____米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com