
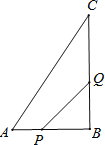
【题目】如图,在△ABC中,∠B=90°,AB=6,BC=8.点P从点A开始沿边AB向点B以1cm/s的速度移动,与此同时,点Q从点B开始沿边BC向点C以2cm/s的速度移动.设P、Q分别从A、B同时出发,运动时间为t,当其中一点先到达终点时,另一点也停止运动.解答下列问题:
(1)经过几秒,△PBQ的面积等于8cm2?
(2)是否存在这样的时刻t,使线段PQ恰好平分△ABC的面积?若存在,求出运动时间t;若不存在,请说明理由.
【答案】(1)2;(2)线段PQ不能平分△ABC的面积.
【解析】
试题(1)设出运动所求的时间,可将BP和BQ的长表示出来,代入三角形面积公式,列出等式,可将时间求出;
(2)将△PBQ的面积表示出来,根据△=b2-4ac来判断.
试题解析:解:(1)设经过x秒,△PBQ的面积等于8cm2则:
BP=6-x,BQ=2x,
所以S△PBQ=![]() ×(6-x)×2x=8,即x2-6x+8=0,
×(6-x)×2x=8,即x2-6x+8=0,
可得:x=2或4(舍去),
即经过2秒,△PBQ的面积等于8cm2.
(2)设经过y秒,线段PQ恰好平分△ABC的面积,△PBQ的面积等于12cm2,
S△PBQ=![]() ×(6-y)×2y=12,
×(6-y)×2y=12,
即y2-6y+12=0,
因为△=b2-4ac=36-4×12=-12<0,所以△PBQ的面积不会等于12cm2,则线段PQ不能平分△ABC的面积.


科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 有实数根.
有实数根.
(1)求m的值;
(2)先作![]() 的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
(3)在(2)的条件下,当直线y=2x+n(n≥m)与变化后的图象有公共点时,求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)直接写出点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE,求P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1cm2,则它移动的距离AA′等于( )

A. 0.5cm B. 1cm C. 1.5cm D. 2cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以1cm/秒的速度移动,同时,点Q从点B出发沿BC边向点C以2cm/秒的速度移动。如果P、Q两点在分别到达B.C两点后就停止移动,回答下列问题:
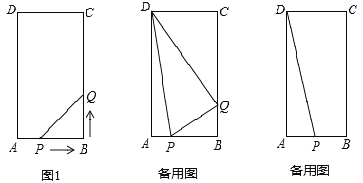
(1)运动开始后第几秒时, △PBQ的面积等于8![]() ?
?
(2)当t=![]() 时,试判断△DPQ的形状。
时,试判断△DPQ的形状。
(3)计算四边形DPBQ的面积,并探索一个与计算结果有关的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
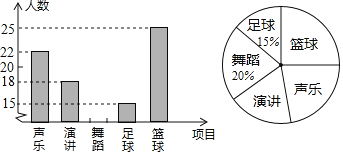
【题目】为丰富学生的文体生活,育红学校准备成立“声乐、演讲、舞蹈、足球、篮球”五个社团,要求每个学生都参加一个社团且每人只能参加一个社团.为了了解即将参加每个社团的大致人数,学校对部分学生进行了抽样调查在整理调查数据的过程中,绘制出如图所示的两幅不完整的统计图,请你根据图中信息解答下列问题:
(1)被抽查的学生一共有多少人?
(2)将条形统计图补充完整.
(3)若全校有学生1500人,请你估计全校有意参加“声乐”社团的学生人数.
(4)从被抽查的学生中随意选出1人,该学生恰好选择参加“演讲”社团的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程(c+a)x2+2bx+(c-a)=0,其中a、b、c分别为△ABC三边的长.
(1)如果方程有两个相等的实数根,试判断△ABC的形状并说明理由;
(2)已知a:b:c=3:4:5,求该一元二次方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场一种商品的进价为每件30元,售价为每件40元.每天可以销售48件,为尽快减少库存,商场决定降价促销.
(1)若该商品连续两次下调相同的百分率后售价降至每件32.4元,求两次下降的百分率;
(2)经调查,若每降价0.5元,每天可多销售4件,那么每天要想获得510元的利润,每件应降价多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若△ABC中,其中一个内角是另一个内角的一半,则称△ABC为“半角三角形”.
(1)若Rt△ABC为半角三角形,∠A=90°,则其余两个角的度数为.
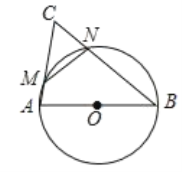
(2)如图,以△ABC的边AB为直径画圆,与边AC交于M,与边BC交于N,已知CN=![]() AC
AC
①求证:∠C=60°.
②若△ABC是半角三角形,求∠B的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com