
����Ŀ��һ���쳵�Ӽؿ����ҵأ�һ���������ҵؿ����أ�����ͬʱ��������쳵���ҵصľ���Ϊy1��km�����������ҵصľ���Ϊy2��km����������ʻʱ��Ϊx��h��������֮��ľ���Ϊs��km����y1��y2��x�ĺ�����ϵͼ����ͼ1��ʾ��s��x�ĺ�����ϵͼ����ͼ2��ʾ���������жϣ���ͼ1��a��3���ڵ�x��![]() hʱ�������������۵�x��
hʱ�������������۵�x��![]() ʱ���������60km����ͼ2��C������Ϊ��3��180�����ݵ�x��
ʱ���������60km����ͼ2��C������Ϊ��3��180�����ݵ�x��![]() h��
h��![]() hʱ���������200km��������ȷ����_____����д��������ȷ�жϵ���ţ�
hʱ���������200km��������ȷ����_____����д��������ȷ�жϵ���ţ�

���𰸡��٢ڢܣ�
��������
����S��x֮��ĺ�����ϵʽ���Եõ���λ��C��ʱ������֮��ľ������ӱ仺����ʱ�쳵��վ����ʱa=3���ʢ���ȷ������������֪y1=y2���з������ɵ�x��ֵΪ![]() ���ʢ���ȷ��������������ǣ�����ǰ���������������60km��x��
���ʢ���ȷ��������������ǣ�����ǰ���������������60km��x��![]() ������ǰ��ʱ�䣬�ʢ���ȷ����ȷ��b��ֵ�����ݺ�����ͼ����Եõ�C�ĵ�����꣬�ʢ���ȷ������������ǰ����������������������ۣ��������x��ֵ����x=
������ǰ��ʱ�䣬�ʢ���ȷ����ȷ��b��ֵ�����ݺ�����ͼ����Եõ�C�ĵ�����꣬�ʢ���ȷ������������ǰ����������������������ۣ��������x��ֵ����x=![]() hʱ�������⣬�ʢݲ���ȷ��
hʱ�������⣬�ʢݲ���ȷ��
�⣺����S��x֮��ĺ�����ͼ���֪����λ��C��ʱ������֮��ľ������ӱ仺��
���ɴ˿��Եõ�a��3���ʢ���ȷ��
��y1��kx+b������0��300������3��0�����룬
�ã�![]() ����ã�
����ã�![]() ��
��
��y1����100x+300��
��y2��mx��
���㣨5��300�����룬�ã�5m��300��
��ã�m��60��
���������ҵصľ���y2����ʽΪ��y2��60x��
�൱y1��y2ʱ������������
�ɵã���100x+300��60x��
��ã�x��![]() h���ʢ���ȷ��
h���ʢ���ȷ��
������������ǣ�����ǰ�������60km��
��100x+300��60x��60����ã�x=![]() h��
h��
�������������60km��
60x������100x+300����60����ã�x=![]() h��
h��
�൱x��![]() h��
h��![]() hʱ���������60km���ʢ۲���ȷ��
hʱ���������60km���ʢ۲���ȷ��
�쳵ÿСʱ��ʻ![]() ��100ǧ�ף�����ÿСʱ��ʻ60ǧ�ף�����֮��ľ���Ϊ300ǧ�ף�
��100ǧ�ף�����ÿСʱ��ʻ60ǧ�ף�����֮��ľ���Ϊ300ǧ�ף�
��b��300����100+60����![]() ��
��
�ɺ�����ͼ����Եõ�C�ĵ�ĺ�����Ϊ3�����쳵�����ҵأ���ʱ�������ߵ�·��Ϊ3��60��180ǧ�ף�
��C������Ϊ��3��180�����ʢ���ȷ��
������������ǣ�����ǰ�������200km��
��100x+300��60x��200����ã�x=![]() h��
h��
�������������60km��
60x������100x+300����200����ã�x=![]() h��
h��
��![]() >3��
>3��
�൱x=![]() h�������⣬��ȥ��
h�������⣬��ȥ��
�൱x��![]() hʱ���������200km���ʢݲ���ȷ��
hʱ���������200km���ʢݲ���ȷ��
�ʴ�Ϊ���٢ڢܣ�


 �ܿ�����ĩ��̾�ϵ�д�
�ܿ�����ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������![]() ����
����![]() ��
��![]() ����
����![]() ���ཻ�ڵ�
���ཻ�ڵ�![]() .
.
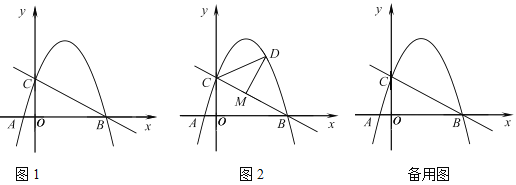
��1���������ߵĽ���ʽ��
��2����![]() ���������ϴ��ڵ�
���������ϴ��ڵ�![]() ��ʹ��
��ʹ��![]() �ǵ��������Σ��������
�ǵ��������Σ��������![]() �����ꣻ
�����ꣻ
��3����ͼ2����![]() ��ֱ��
��ֱ��![]() �Ϸ��������ϵ�һ������.����
�Ϸ��������ϵ�һ������.����![]() ��
��![]() �ڵ�
�ڵ�![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() �е�ij����ǡ�õ���
�е�ij����ǡ�õ���![]() ��2���������ڣ��������
��2���������ڣ��������![]() �ĺ����ꣻ�������ڣ���˵������.
�ĺ����ꣻ�������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
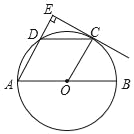
����Ŀ����ͼ��ʾ��AB�ǡ�O��ֱ������D�ǻ�AC���е㣬��COB��60��������C��CE��AD����AD���ӳ����ڵ�E��
��1����֤��CEΪ��O�����ߣ�
��2����CE��![]() �����O�İ뾶����
�����O�İ뾶����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y��a��x+1����x��3����x�ύ��A��B���㣬��������x��Χ�ɵķ�����������߽磩������4��������ʱ����������Ǻ��������Ϊ�����ĵ㣩����a��ȡֵ��Χ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�У���A�ڷ���������y=![]() ��k��0����ͼ���ϣ���D��y���ϣ���B����C��x���ϣ���ƽ���ı���ABCD�����Ϊ10����k��ֵ�ǣ�������
��k��0����ͼ���ϣ���D��y���ϣ���B����C��x���ϣ���ƽ���ı���ABCD�����Ϊ10����k��ֵ�ǣ�������
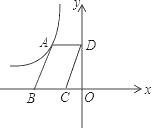
A. ��10 B. ��5 C. 5 D. 10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�ڵĵ�M����ᡢ�����궼Ϊ��������ѵ�M�����������������磺P��1��0����Q��2����2����������������������y��mx2��4mx+4m��2��m��0����x�ύ�ڵ�A��B���㣬������������A��B֮��IJ������߶�AB��Χ�ɵ��������߽磩ǡ���߸����㣬��m��ȡֵ��Χ�ǣ�������
A. ![]() ��m��1B.
��m��1B. ![]() ��m��1C. 1��m��2D. 1��m��2
��m��1C. 1��m��2D. 1��m��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c�����㣨��1��0�����Գ���l��ͼ��ʾ�������н��ۣ���abc��0����a��b+c=0����2a+c��0����a+b��0������������ȷ�Ľ����ǣ� ��
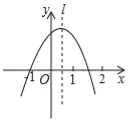
A���٢� B���ڢ� C���ڢ� D���ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
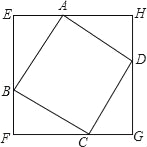
����Ŀ����ͼ��������ABCD���ĸ�����ֱ���������EFGH���������ϣ����dz�������EFGH��������ABCD����������Σ�
̽��һ����֪�߳�Ϊ1��������ABCD���Ƿ����һ�����������EFGH�����������������ABCD�����2������ͼ���������������EFGH�����������������ABCD��2����
��Ϊ������ABCD�����Ϊ1����������EFGH�����Ϊ2��
����EF=FG=GH=HE=![]() ����EB=x����BF=
����EB=x����BF=![]() ��x��
��x��
��Rt��AEB��Rt��BFC
��BF=AE=![]() ��x
��x
��Rt��AEB�У��ɹ��ɶ�������
x2+��![]() ��x��2=12
��x��2=12
��ã�x1=x2=![]()
��BE=BF������B��EF���е㣮
ͬ������C��D��A�ֱ���FG��GH��HE���е㣮
���ԣ�����һ�����������EFGH�����������������ABCD�����2��
̽��������֪�߳�Ϊ1��������ABCD���Ƿ����һ�����������EFGH�����������������ABCD�����3�����������������������̽�����̣�
̽��������֪�߳�Ϊ1��������ABCD���� ��һ�����������EFGH�����������������ABCD�����4����������ڡ������ڡ���
̽���ģ���֪�߳�Ϊ1��������ABCD���Ƿ����һ�����������EFGH�����������������ABCD�����n������n��2���������������������̽�����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
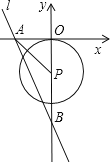
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l��y=-2x-8�ֱ���x�ᣬy���ཻ��A��B���㣬��P��0��k����y��ĸ������ϵ�һ�����㣬��PΪԲ�ģ�3Ϊ�뾶����P��
��1������P��x���й����㣬��k��ȡֵ��Χ��______��
��2������PA����PA=PB�����жϡ�P��x���λ�ù�ϵ����˵�����ɣ�
��3������P��ֱ��l����ʱ��k��ֵΪ______��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com