
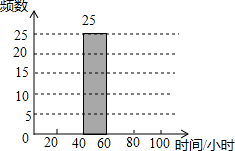
 2015年12月18日天津日报报道,美国哈佛大学的学者们在进行了长达二十多年的跟踪研究之后,得出了一个惊人的结论:爱干家务的孩子与不爱干家务的孩子相比,失业率比例为1:15,犯罪率的比例为1:10.某校要求学生们寒假在家帮助父母做些力所能及的家务,李翰同学在开学初对本校部分学生寒假期间在家做家务的时间进行了抽样调查(时间取整小时),整理数据后绘制成频数分布表如图所示的频数分布直方图.
2015年12月18日天津日报报道,美国哈佛大学的学者们在进行了长达二十多年的跟踪研究之后,得出了一个惊人的结论:爱干家务的孩子与不爱干家务的孩子相比,失业率比例为1:15,犯罪率的比例为1:10.某校要求学生们寒假在家帮助父母做些力所能及的家务,李翰同学在开学初对本校部分学生寒假期间在家做家务的时间进行了抽样调查(时间取整小时),整理数据后绘制成频数分布表如图所示的频数分布直方图. | 时间段(小时) | 频数 | 频率 |
| 0-20 | ||
| 20-40 | 20 | 25% |
| 40-60 | 25 | |
| 60-80 | 15 | |
| 80-100 | 12.5% |
分析 (1)根据20-40段的频数是40,对应的百分比是25%,据此即可求得调查的总人数,进而求得0-20段和80-100段的人数,从而补全直方图;
(2)求出62%的学生人数,确定所在的组即可.
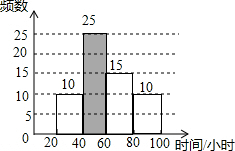
解答 解:(1)调查的总人数是20÷25%=80(人),
则80-100小时段的频数是80×12.5%=10(人),
则0-20小时段的频数是80-20-25-15-10=10(人).
| 时间段(小时) | 频数 | 频率 |
| 0-20 | 10 | 12.5% |
| 20-40 | 20 | 25% |
| 40-60 | 25 | 31.25% |
| 60-80 | 15 | 18.75% |
| 80-100 | 10 | 12.5% |
 ;
;点评 本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 众数是30 | B. | 中位数是31 | C. | 平均数是33 | D. | 极差是35 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com