
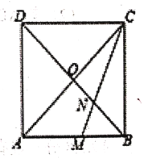
【题目】如图,正方形![]() 的对角线
的对角线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 的角平分线分别交
的角平分线分别交![]() 、
、![]() 于
于![]() 、
、![]() 两点.若
两点.若![]() ,则线段
,则线段![]() 的长为( )
的长为( )
A.![]() B.
B.![]() C.1D.
C.1D.![]()
【答案】A
【解析】
过点M作ME⊥AC于E,根据正方形的性质和锐角三角函数即可求出AE=EM=1,△CON∽△CEM,再根据角平分线的性质可得BM=EM=1,从而求出正方形的边长,即可求出对角线AC的长,然后根据相似三角形的性质列出比例式即可求出ON.
解:过点M作ME⊥AC于E
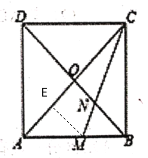
∵正方形![]() 的对角线
的对角线![]() 与
与![]() 相交于点
相交于点![]()
∴∠CAB=45°,∠COB=∠ABC=90°,AB=BC,CO=AO=![]()
∴△AEM为等腰三角形,OB∥EM
∴AE=EM=AM·sin∠EAM=![]() ,△CON∽△CEM,
,△CON∽△CEM,
∵CM平分∠ACB
∴BM=EM=1
∴AB=AM+MB=![]()
在Rt△ABC中,AC=![]()
∴CE=AC-AE=![]() ,CO=
,CO=![]()
∵△CON∽△CEM
∴![]()
即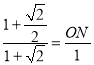
解得:ON=![]()
故选A.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
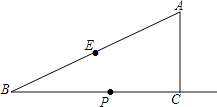
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,E为斜边AB的中点,点P是射线BC上的一个动点,连接AP、PE,将△AEP沿着边PE折叠,折叠后得到△EPA′,当折叠后△EPA′与△BEP的重叠部分的面积恰好为△ABP面积的四分之一,则此时BP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
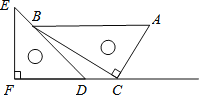
【题目】一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,则CD=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解决问题:
材料1:在研究数的整除时发现:能被5、25、125、625整除的数的特征是:分别看这个数的末一位、末两位、末三位、末四位即可,推广成一条结论;末![]() 位能被
位能被![]() 整除的数,本身必能被
整除的数,本身必能被![]() 整除,反过来,末
整除,反过来,末![]() 位不能被
位不能被![]() 整除的数,本身也不可能被
整除的数,本身也不可能被![]() 整除,例如判断992250能否被25、625整除时,可按下列步骤计算:
整除,例如判断992250能否被25、625整除时,可按下列步骤计算:
![]() ,
,![]() 为整数,
为整数,![]() 能被25整除
能被25整除
![]() ,
,![]() 不为整数,
不为整数,![]() 不能被625整除
不能被625整除
材料2:用奇偶位差法判断一个数能否被11这个数整除时,可把这个数的奇位上的数字与偶位上的数字分别加起来,再求它们的差,看差能否被11整除,若差能被11整除,则原数能被11整除,反之则不能.
(1)若![]() 这个三位数能被11整除,则
这个三位数能被11整除,则![]() ;在该三位数末尾加上和为8的两个数字,让其成为一个五位数,该五位数仍能被11整除,求这个五位数
;在该三位数末尾加上和为8的两个数字,让其成为一个五位数,该五位数仍能被11整除,求这个五位数
(2)若一个六位数p的最高位数字为5,千位数字是个位数字的2倍,且这个数既能被125整除,又能被11整除,求这个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,
中,![]() 为
为![]() 边上一点
边上一点![]() ,
,![]() .将
.将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,
,![]() 的延长线交边
的延长线交边![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
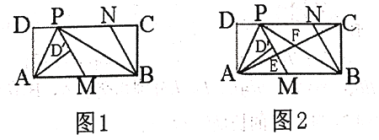
(1)求证:![]() ;
;
(2)如图2,连接![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .若
.若![]() ,探究
,探究![]() 与
与![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形![]() 为正方形,点
为正方形,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,且
轴上,且![]() ,
,![]() ,反比例函数
,反比例函数![]() 在第一象限的图象经过正方形的顶点
在第一象限的图象经过正方形的顶点![]() .
.

(1)求点![]() 的坐标和反比例函数的关系式.
的坐标和反比例函数的关系式.
(2)如图2,将正方形![]() 沿
沿![]() 轴向右平移 个单位长度时,点
轴向右平移 个单位长度时,点![]() 恰好落在反比例函数的图象.
恰好落在反比例函数的图象.
(3)在(2)的情况下,连接![]() 并延长,交反比例函数的图象于点
并延长,交反比例函数的图象于点![]() ,点
,点![]() 是
是![]() 轴上的一个动点(不与点
轴上的一个动点(不与点![]() 、
、![]() 重合)
重合)
①当点![]() 的坐标为多少时,四边形
的坐标为多少时,四边形![]() 是矩形?请说明理由.
是矩形?请说明理由.
②过点![]() 作
作![]() 轴于点
轴于点![]() ,请问当点
,请问当点![]() 的坐标为多少时,
的坐标为多少时,![]() 与
与![]() 相似?(直接写出答案).
相似?(直接写出答案).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com