
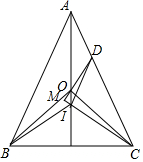
 △ABC中,AB=AC,O、I分别是其外心、内心,点D在AC上,且DI∥AB,DO的延长线交CI的延长线于M.求证:DM⊥CM.
△ABC中,AB=AC,O、I分别是其外心、内心,点D在AC上,且DI∥AB,DO的延长线交CI的延长线于M.求证:DM⊥CM. 分析 先用平行线的性质和三角形的外角的性质得出∠AID=∠CAM,进而得出点O,I,C,D四点共圆,再用直角三角形的两锐角互余即可得出结论.
解答 证明: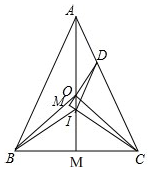
∵O是△ABC的外心,AB=AC,
∴AM⊥BC,
∴∠CAM=$\frac{1}{2}$∠BAC,
∵DI∥AB,
∴∠IDC=∠BAC=2∠CAM,
∵∠IDC=∠CAM+∠ADO(三角形的一个外角等于与它不相邻的两内角的和),
∴∠AID=∠CAM,
∵O是△ABC的外心,
∴OA=OC,
∴∠ACO=∠CAM,
∴∠AID=∠ACO,
∴点O,I,C,D四点共圆,
∴∠ODI=∠OCI,
∵I是△ABC的内心,
∴∠ACI=∠ICM,
∵OA=OC,
∴∠COM=2∠CAM,
在Rt△COM中,∠COM+∠OCM=90°,
∴∠ODC+∠ACI
=∠ODI+∠IDC+∠ACI
=∠OCI+2∠CAM+∠ACM
=∠COM+∠OCM
=90°,
∴∠CMD=90°,
∴DM⊥CM.
点评 此题是三角形五心,主要考查了三角形内心与外心的性质、圆周角定理、四点共圆的判定方法和等腰三角形的性质;判断点O,I,C,D四点共圆是解本题的关键.


科目:初中数学 来源: 题型:解答题
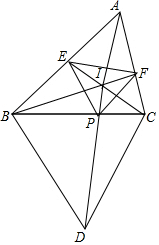 如图,△ABC中,∠A=60°,以BC为边往外作等边△BCD,作∠B,∠C的角平分线分别交AC,AB于点F,E,若BE,CF交于点I,连接ID交BC于点P,求证:△EFP为等边三角形.
如图,△ABC中,∠A=60°,以BC为边往外作等边△BCD,作∠B,∠C的角平分线分别交AC,AB于点F,E,若BE,CF交于点I,连接ID交BC于点P,求证:△EFP为等边三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
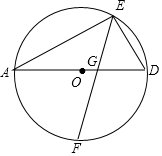 以AD为直径作⊙O,F是半圆弧$\widehat{AD}$上中点,E是半圆弧$\widehat{AD}$上一点,EA=8,ED=6,连接EF交AD于点G,求tan∠AGF的值.
以AD为直径作⊙O,F是半圆弧$\widehat{AD}$上中点,E是半圆弧$\widehat{AD}$上一点,EA=8,ED=6,连接EF交AD于点G,求tan∠AGF的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
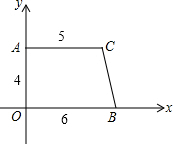 如图,在直角梯形AOBC中,AC平行于OB,且OB=6,AC=5,OA=4,
如图,在直角梯形AOBC中,AC平行于OB,且OB=6,AC=5,OA=4,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
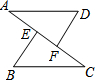 如图,在△AFD和△CEB中,点A、E、F、C在同一条直线上,有下列四个判断:①AD=CB;②AE=CF;③∠B=∠D;④∠A=∠C.请以其中三个为已知条件,剩下一个作为结论,编一道数学题(用序号???⇒?的形式写出),并写出证明过程.
如图,在△AFD和△CEB中,点A、E、F、C在同一条直线上,有下列四个判断:①AD=CB;②AE=CF;③∠B=∠D;④∠A=∠C.请以其中三个为已知条件,剩下一个作为结论,编一道数学题(用序号???⇒?的形式写出),并写出证明过程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com