
【题目】△ABC在下列条件下,不是直角三角形的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】B
【解析】
利用勾股定理的逆定理判断A、D选项,用直角三角形各角之间的关系判断B、C选项.
解:A、∵b2=a2-c2,∴b2+c2=a2,故本选项正确;
B、∵∠A:∠B:∠C=3:4:5,∴设∠A=3x,则∠B=4x,∠C=5x,
∵∠A+∠B+∠C=180°,即3x+4x+5x=180°,解得,x=15°,
∴5x=5×15°=75°<90°,故本选项错误.
C、∵∠A=∠B-∠C,∴∠B=∠A+∠C,
∵∠A+∠B+∠C=180°,∴2(∠A+∠C)=180°,即∠A+∠C=90°,故本选项正确;
D、∵a2:b2:c2=1:3:2,∴令a2=x,则b2=2x,c2=3x,
∵x+2x=3x,∴a2+c2=b2,故本选项正确;
故选:B.


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,∠1=∠2,DB=DC.
(1)求证:△ABD≌△EDC;
(2)若∠A=135°,∠BDC=30°,求∠BCE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
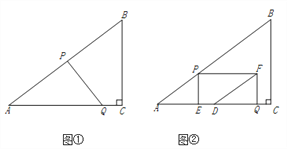
【题目】如图①,在Rt△ABC中,∠C=90°,AB=10,BC=6.点P从点A出发,沿折现AB—BC向终点C运动,在AB上以每秒5个单位长度的速度运动,在BC上以每秒3个单位长度的速度运动.点Q从点C出发,沿CA方向以每秒![]() 个单位长度的速度运动.点P、Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.
个单位长度的速度运动.点P、Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.
(1)求线段AQ的长.(用含t的代数式表示)
(2)当PQ与△ABC的一边平行时,求t的值
(3)如图②,过点P作PE⊥AC于点E,以PE、QE为邻边作矩形PEQF,点D为AC的中点,连结DF.直接写出DF将矩形PEQF分成两部分的面积比为1:2时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的推理过程,在括号内填上推理的依据,如图:

∵∠1+∠2=180°,∠2+∠4=180°(已知)
∴∠1=∠4( )
∴c∥a( )
又∵∠2+∠3=180°(已知 )
∠3=∠6( )
∴∠2+∠6=180°( )
∴a∥b( )
∴c∥b( )
查看答案和解析>>
科目:初中数学 来源: 题型:
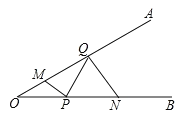
【题目】如图,∠AOB=30°,M、N分别在OA、OB上,且OM=2,ON=4,点P、Q分别在OB、OA上,则MP+PQ+QN的最小值是 _______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ∠B、∠D的两边分别平行。
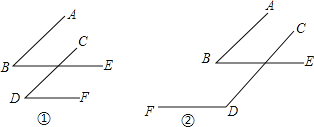
(1)在图1中,∠B与∠D的数量关系是 ;在图2中,∠B与∠FDC的数量关系是 ;
(2)用一句话归纳的结论为: ;
(3)已知∠α的两边与∠β的两边分别平行,并且∠α比∠β的3倍少![]() ,求∠α、∠β的度数.
,求∠α、∠β的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于![]() 长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.

(1)四边形ABEF是_______;(选填矩形、菱形、正方形、无法确定)(直接填写结果)
(2)AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为________,∠ABC=________°.(直接填写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | n |
80≤x<90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
请根据所给信息,解答下列问题:
(1)m= ,n= ;
(2)请补全频数分布直方图;
(3)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com