
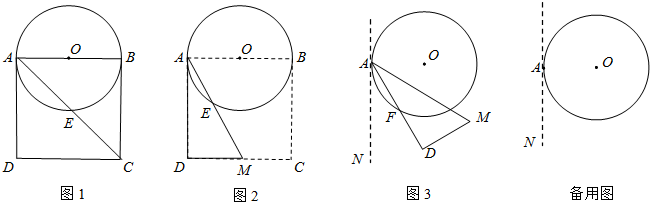
分析 (1)连接BE,则可得出△AEB是等腰直角三角形,再由AB=8,可得出AE的长.
(2)①连接OA、OF,可判断出△OAF是等边三角形,从而可求出AF的长;②此时可得DAM=30°,根据AD=8可求出AF的长,也可判断DM与⊙O的位置关系;③根据AD等于⊙O的直径,可得出当DM与⊙O相切时,点D在⊙O上,从而可得出α的度数.
解答 解:(1)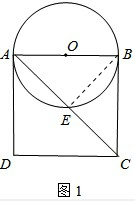
连接BE,
∵AC是正方形ABCD的对角线,
∴∠BAC=45°,
∴△AEB是等腰直角三角形,
又∵AB=8,
∴AE=4$\sqrt{2}$;
(2)①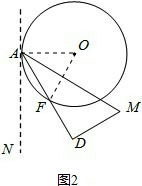
连接OA、OF,
由题意得,∠NAD=30°,∠DAM=30°,
故可得∠OAM=30°,∠DAM=30°,
则∠OAF=60°,
又∵OA=OF,
∴△OAF是等边三角形,
∵OA=4,
∴AF=OA=4;
②
连接B'F,此时∠NAD=60°,
∵AB'=8,∠DAM=30°,
∴AF=AB'cos∠DAM=8×$\frac{\sqrt{3}}{2}$=4$\sqrt{3}$;
此时DM与⊙O的位置关系是相离;
③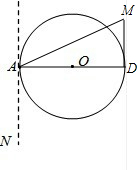
∵AD=8,直径的长度相等,
∴当DM与⊙O相切时,点D在⊙O上,
故此时可得α=∠NAD=90°.
点评 此题属于圆的综合题,主要是仔细观察每一次旋转后的图形,根据含30°角的直角三角形进行计算,另外在解答最后一问时,关键是判断出点D的位置,有一定难度.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:解答题
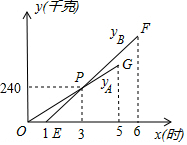 为了保证安全,某仓库引进A型、B型两台机器人搬运某种有毒货物到仓库存放,这两台机器人充满电后,各能连续工作5h,按照指令,A型机器人于某日零时开始搬运,过了1h,B型机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(kg)与A型机器人搬运时间x(h)之间的关系图象,线段EF表示B种机器人的搬运量yB(kg)与A型机器人的时间x(h)之间的关系图象,根据图象提供的信息解答下列问题:
为了保证安全,某仓库引进A型、B型两台机器人搬运某种有毒货物到仓库存放,这两台机器人充满电后,各能连续工作5h,按照指令,A型机器人于某日零时开始搬运,过了1h,B型机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(kg)与A型机器人搬运时间x(h)之间的关系图象,线段EF表示B种机器人的搬运量yB(kg)与A型机器人的时间x(h)之间的关系图象,根据图象提供的信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
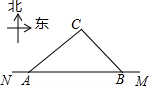 2016年我市荣获“国家卫生城市称号”在创卫过程中,要在东西方向,M、N两地之间修建一条道路,已知如图C点周围180cm范围内为文物保护区,在MN上点A处测得C在A的北偏东60°的方向上,从A向东走500m到达B处,测得C在B的北偏西45°方向上
2016年我市荣获“国家卫生城市称号”在创卫过程中,要在东西方向,M、N两地之间修建一条道路,已知如图C点周围180cm范围内为文物保护区,在MN上点A处测得C在A的北偏东60°的方向上,从A向东走500m到达B处,测得C在B的北偏西45°方向上查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 成绩/m | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
| 人数 | 2 | 3 | 2 | 3 | 4 | 1 |
| A. | 1.70、1.75 | B. | 1.70、1.80 | C. | 1.65、1.75 | D. | 1.65、1.80 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1或-5 | B. | -1或5 | C. | 1或-3 | D. | 1或3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售单价(元) | x |
| 销售量y(件) | -10x+800 |
| 销售玩具获得利润w(元) | -10x2+1000x-16000 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
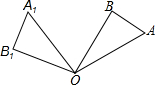 如图,在Rt△OAB中,∠AOB=30°,将△OAB绕点O逆时针旋转100°,得到△OA1B1,求∠A1OB的度数( )
如图,在Rt△OAB中,∠AOB=30°,将△OAB绕点O逆时针旋转100°,得到△OA1B1,求∠A1OB的度数( )| A. | 100° | B. | 70° | C. | 40° | D. | 30° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com