
【题目】如图,直线y=-x+3与x轴,y轴分别交于B,C两点,抛物线y=-x2+bx+c经过B,C两点,点A是抛物线与x轴的另一个交点.
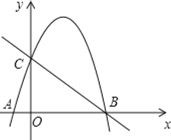
(1)求此抛物线的函数解析式;
(2)在抛物线上是否存在点P,使S△PAB=2S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在这样的P点,且坐标为:(
;(2)存在这样的P点,且坐标为:(![]() ,
,![]() ),(
),(![]() ,
,![]() )
)
【解析】
(1)首先求出B、C两点的坐标,然后进一步代入抛物线解析式加以求解即可;
(2)首先根据抛物线解析式求出A点坐标,从而得出AB=4,求出△CAB的面积为6,然后设P点坐标为(![]() ,
,![]() ),根据题意进一步列出方程加以分析求解即可.
),根据题意进一步列出方程加以分析求解即可.
(1)∵直线![]() 经过B、C两点,
经过B、C两点,
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
∴B点坐标为(3,0),C点坐标为(0,3),
又∵抛物线![]() 经过B、C两点,
经过B、C两点,
∴![]() ,
,
解得:![]() ,
,![]() ,
,
∴该抛物线解析式为:![]() ;
;
(2)当![]() 时,
时,![]() ,
,
∴![]() ,
,![]() ,
,
∴A点坐标为(![]() ,0),
,0),
∴AB=4,
∴△CAB的面积=![]() ,
,
设P点坐标为(![]() ,
,![]() ),
),
∵S△PAB=2S△CAB,
则:![]() ,
,
∴![]() ,
,
即![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,此时方程无解,
,此时方程无解,
∴此时P点不存在,
当![]() 时,
时,![]() ,解得:
,解得:![]() ,
,![]() ,
,
∴此时P点坐标为(![]() ,
,![]() ),(
),(![]() ,
,![]() ),
),
综上所述,存在这样的P点,且坐标为:(![]() ,
,![]() ),(
),(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
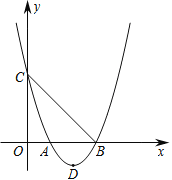
【题目】如图,抛物线y=ax2-4ax+b交x轴正半轴于A、B两点,交y轴正半轴于C,且OB=OC=3.
(1) 求抛物线的解析式;
(2) 如图1,D为抛物线的顶点,P为对称轴左侧抛物线上一点,连接OP交直线BC于G,连GD.是否存在点P,使![]() ?若存在,求点P的坐标;若不存在,请说明理由;
?若存在,求点P的坐标;若不存在,请说明理由;
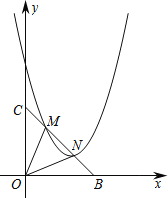
(3) 如图2,将抛物线向上平移m个单位,交BC于点M、N.若∠MON=45°,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象交x轴于A、B两点,交y轴于点D,点B的坐标为
的图象交x轴于A、B两点,交y轴于点D,点B的坐标为![]() ,顶点C的坐标为
,顶点C的坐标为![]() .
.
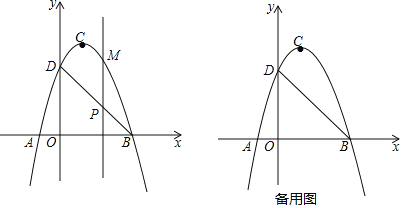
![]() 求二次函数的解析式和直线BD的解析式;
求二次函数的解析式和直线BD的解析式;
![]() 点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;
点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;
![]() 在抛物线上是否存在异于B、D的点Q,使
在抛物线上是否存在异于B、D的点Q,使![]() 中BD边上的高为
中BD边上的高为![]() ?若存在求出点Q的坐标;若不存在请说明理由.
?若存在求出点Q的坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,对角线AC、BD交于O点,DE∥AC,CE∥BD.
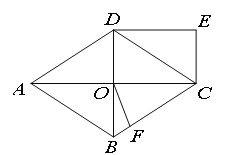
(1)求证:四边形OCED为矩形;
(2)在BC上截取CF=CO,连接OF,若AC=16,BD=12,求四边形OFCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展“我最喜爱的一项体育活动”调查,要求每名学生必选且只能选一项.现随机抽查了部分学生,并将其结果绘制成如下不完整的条形图和扇形图.
抽取的学生最喜欢体育活动的条形统计图
抽取的学生最喜欢体育活动的扇形统计图
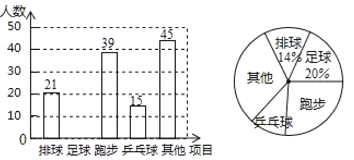
请结合以上信息解答下列问题:
(1)在这次调查中一共抽查了_____学生,扇形统计图中“乒乓球”所对应的圆心角为_____度,并请补全条形统计图;
(2)己知该校共有1200名学生,请你估计该校最喜爱跑步的学生人数;
(3)若在“排球、足球、跑步、乒乓球”四个活动项目任选两项设立课外兴趣小组,请用列表法或画树状图的方法求恰好选中“排球、乒乓球”这两项活动的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业拥有一条生产某品牌酸奶的生产线,已知该酸奶销售额为4800元时的销量比销售额为800元时的销量要多500瓶.现接到一单生产任务,需要在16天内完成,为按时完成任务,该企业招收了新工人甲,设甲第x天(x为整数)生产的酸奶数量为y瓶,y与x满足下列关系式:y=![]() .
.
(1)求每瓶酸奶的售价为多少元?
(2)如图,设第x天每瓶酸奶的成本是p元,已知p与x之间的关系可以用图中的函数图象来刻画.若甲第x天创造的利润为w元,请直接写出w与x之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=售价﹣成本)
(3)设(2)小题中第m天利润达到最大值,若要使第(m+1)天的利润比第m天的利润至少多50元,则第(m+1)天每瓶酸奶至少应提价几元?

查看答案和解析>>
科目:初中数学 来源: 题型:
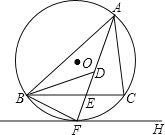
【题目】如图,![]() 是锐角
是锐角![]() 的外接圆,
的外接圆,![]() 是
是![]() 的切线,切点为
的切线,切点为![]() ,
,![]() ,连结
,连结![]() 交
交![]() 于
于![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 于
于![]() ,连结
,连结![]() .下列结论:①
.下列结论:①![]() 平分
平分![]() ;②连接
;②连接![]() ,点
,点![]() 为
为![]() 的外心;③
的外心;③![]() ;④若点
;④若点![]() ,
,![]() 分别是
分别是![]() 和
和![]() 上的动点,则
上的动点,则![]() 的最小值是
的最小值是![]() .其中一定正确的是__________(把你认为正确结论的序号都填上).
.其中一定正确的是__________(把你认为正确结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
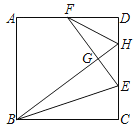
【题目】如图,正方形纸片ABCD沿直线BE折叠,点C恰好落在点G处,连接BG并延长,交CD于点H,延长EG交AD于点F,连接FH.若AF=FD=6cm,则FH的长为_____cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com