
【题目】如图,抛物线经过A(-1,0),B(5,0),C(0,-![]() )三点.
)三点.
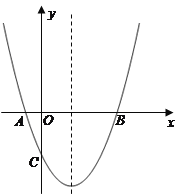
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
【答案】(1)![]() .;(2) (2,-
.;(2) (2,-![]() ).
).
【解析】试题(1)先设所求二次函数的解析式为y=ax2+bx+c(a≠0),再把A(-1,0),B(5,0),C(0,-![]() )入函数解析式,得到关于a、b、c的三元一次方程组,解即可求a、b、c,进而可得函数解析式.
)入函数解析式,得到关于a、b、c的三元一次方程组,解即可求a、b、c,进而可得函数解析式.
(2)连接BC,交对称轴于P,P即为使PA+PC的值最小,设直线BC的解析式,把B、C的坐标代入即可求得系数,进而求得解析式,令x=2时,即可求得P的坐标.
试题解析:(1)设所求二次函数的解析式为y=ax2+bx+c(a≠0),
代入A(-1,0),B(5,0),C(0,-![]() )三点,得
)三点,得
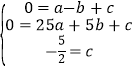 ,
,
解得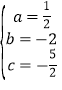 ,
,
所以这个二次函数的解析式是:![]() .
.
(2)∵![]()
=![]()
∴抛物线的对称轴为x=2,
设直线BC的解析式为y=kx+m,
∴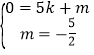
解得 ,
,
∴直线BC的解析式为y=![]() ,
,
当x=2时,y=-![]() ,
,
∴P点的坐标为(2,-![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=﹣1.
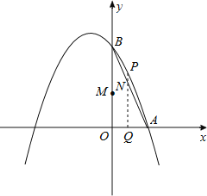
(1)求抛物线对应的函数关系式;
(2)动点Q从点O出发,以每秒1个单位长度的速度在线段OA上运动,同时动点M从M从O点出发以每秒3个单位长度的速度在线段OB上运动,过点Q作x轴的垂线交线段AB于点N,交抛物线于点P,设运动的时间为t秒.
①当t为何值时,四边形OMPQ为矩形;
②△AON能否为等腰三角形?若能,求出t的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为预防禽流感,上海建立了候鸟监测站,某候鸟监测站将一天7点至17点监测到上空飞过的候鸟数制成了如下直方图:
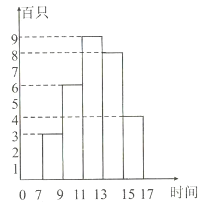
(1)候鸟飞过的高峰期在一天的______;
(2)这一天7点至17点期间,平均每小时飞过上空的候鸟有______只;
(3)每两个小时飞过上空的候鸟数的中位数是______;
(4)若一天飞过上空的候鸟数按此估算,该监测站九月份监测到的候乌只数约是______只;
(5)7时—9时段的频率是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三张正面分别标有数字:-1,1,2的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中随机抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.
(1)请用列表或画树形图的方法(只选其中一种),表示两次抽出卡片上的数字的所有结果;
(2)将第一次抽出的数字作为点的横坐标x,第二次抽出的数字作为点的纵坐标y,求点(x,y)落在双曲线![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的两边长AB=16cm,AD=4cm,点P,Q分别从A,B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动设运动时间为x(秒),设△BPQ的面积为ycm2.
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)当△BPQ面积有最大值时,求x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 和
和![]() 是两个完全重合在一起的等腰直角三角形,
是两个完全重合在一起的等腰直角三角形,![]() .现将
.现将![]() 固定,将
固定,将![]() 绕点
绕点![]() 按逆时针方向旋转,旋转角为
按逆时针方向旋转,旋转角为![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,
,![]() .
.

(1)如图2,当![]() 时,判断四边形
时,判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(2)如图3,当![]() 时,(1)中的结论是否仍然成立?说明理由.
时,(1)中的结论是否仍然成立?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=x2的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…n在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnn都是正方形,则正方形An﹣1BnAnn的周长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】立定跳远是嘉兴市体育中考的抽考项目之一,某校九年级(1),(2)班准备集体购买某品牌的立定跳远训练鞋.现了解到某网店正好有这种品牌训练鞋的促销活动,其购买的单价y(元/双)与一次性购买的数量x(双)之间满足的函数关系如图所示.
(1)当10≤x<60时,求y关于x的函数表达式;
(2)九(1),(2)班共购买此品牌鞋子100双,由于某种原因需分两次购买,且一次购买数量多于25双且少于60双;
①若两次购买鞋子共花费9200元,求第一次的购买数量;
②如何规划两次购买的方案,使所花费用最少,最少多少元?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com