练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．计算：2sin45°-（$π-\sqrt{5}$）0$+（\frac{1}{2}）^{-1}$$+|\sqrt{2}-1|$．

    分析 原式第一项利用特殊角的三角函数值计算，第二项利用零指数幂法则计算，第三项利用负整数指数幂法则计算，最后一项利用绝对值的代数意义化简，计算即可得到结果．

    解答 解：原式=2×$\frac{\sqrt{2}}{2}$-1+2+$\sqrt{2}$-1
    =2$\sqrt{2}$．

    点评 此题考查了实数的运算，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

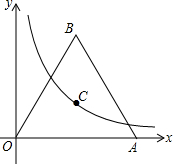    4．如图，在平面直角坐标系中，双曲线y=$\frac{\sqrt{3}}{x}$（x＞0）上的一点C过等边三角形OAB三条高的交点，则点B的坐标为（$\sqrt{3}$，$\sqrt{3}$+1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

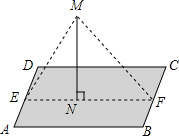    5．“五一期间”某公司在一块平行四边形ABCD的湖中，立有一个旗杆MN，MN与湖面垂直，旗杆顶端M与湖岸的E、F两处用绳子相连．绳子上系满了彩旗．且直线EF经过旗杆底部N，EF∥AB，已知，AB=40（$\sqrt{3}$+1）m．BC=30m．∠MEN=60°，∠MFN=45°，求绳子EM的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．在平面直角坐标系xOy中，点P（a，b）的“变换点”Q的坐标定义如下：当a≥b时，Q点坐标为（b，-a）；当a＜b时，Q点坐标为（a，-b）．
    （1）求（-2，3），（6，-1）的变换点坐标；
    （2）已知直线l与x轴交于点A（4，0），与y轴交于点B（0，2）．若直线l上所有点的变换点组成一个新的图形，记作图形W，请画出图形W，并简要说明画图的思路；
    （3）若抛物线y=-$\frac{3}{4}$x2+c与图形W有三个交点，请直接写出c的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．（1）计算：$\frac{1}{\sqrt{3}}-\root{3}{8}$+|2-$\sqrt{3}$|；
    （2）当关于x的方程x2-2x+c=0有实数根时，求c的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．在一次60秒跳绳测试中，10名同学跳的次数分别为170，190，180，150，180，180，160，200，180，190，则这次测试所跳次数的众数为180．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．有两个构造完全相同（除所标数字外）的转盘A、B．
    （1）单独转动A盘，指向奇数的概率是$\frac{2}{3}$；
    （2）小红和小明做了一个游戏，游戏规定，转动两个转盘各一次，两次转动后指针指向的数字之和为奇数则小红获胜，数字之和为偶数则小明获胜，请用树状图或列表说明谁获胜的可能性大．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．甲、乙、丙、丁四位同学在三次数学测验中，他们成绩的平均分都是85分，方差分别是S甲2=3.8，S乙2=2.3，S丙2=6.2，S丁2=5.2，则成绩最稳定的是（　　）
    A．甲B．乙C．丙D．丁

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

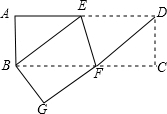    4．如图，将矩形纸片ABCD沿EF折叠，使D与B重合，折痕为EF，然后展开，连接DF，BE．
    （1）求证：四边形EBFD是菱形；
    （2）已知AB=3，AD=9，求折痕EF的长．

    查看答案和解析>>

    同步练习册答案