练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图1，扇形AOB中，OA=10，∠AOB=36°．若固定B点，将此扇形依顺时针方向旋转，得一新扇形A′O′B，其中A点在O′B上，如图2所示，则O点旋转至O′点所经过的轨迹长度为（ ）

    A．π
    B．2π
    C．3π
    D．4π
    【答案】分析：根据弧长公式，此题主要是得到∠OBO′的度数．根据等腰三角形的性质即可求解．
    解答：解：根据题意，知OA=OB．
    又∵∠AOB=36°，
    ∴∠OBA=72°．
    ∴点旋转至O′点所经过的轨迹长度==4π．
    故选D．
    点评：此题综合运用了等腰三角形的性质和弧长公式．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图1，扇形AOB中，OA=10，∠AOB=36°．若固定B点，将此扇形依顺时针方向旋转，得一新扇形A′O′B，其中A点在O′B上，如图2所示，则O点旋转至O′点所经过的轨迹长度为（　　）
    精英家教网
    A、πB、2πC、3πD、4π

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图1，扇形AOB中，∠AOB=120°，C为半径OA上一点，CD∥OB，交
    AB
    于D点．
    （1）当CD=6，AC=1时，直接写出半径OB的长，以及CD与OB的大小关系；
    （2）在图1中画出以OA，OB为邻边的菱形AOBE，并说明E点的位置；（不要求写菱形AOBE的画法）
    （3）若将图1中扇形的圆心角∠AOB改为105°（如图2），C仍为半径OA上一点（C点不与O，A两点重合），CD∥OB，交
    AB
    于D点，在图2中画图说明满足CD≤OB时D点运动的范围．

    查看答案和解析>>

    科目：初中数学 来源：2010年高级中等学校招生全国统一考试数学卷（山东济宁） 题型：单选题

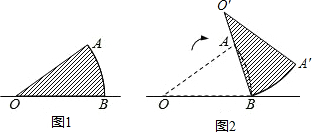
    如图(十三)，扇形AOB中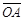，=10， ÐAOB=36°。若固定B点，将此扇形依顺时针方向旋转，得一新扇形A’O’B，其中A点在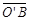上，如图(十四)所示，则O点旋转至O’点所经过的轨迹长度为何？

    查看答案和解析>>

    科目：初中数学 来源：2010年高级中等学校招生全国统一考试数学卷（山东济宁） 题型：选择题

    如图(十三)，扇形AOB中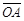，=10， ÐAOB=36°。若固定B点，将此扇形依顺时针方向旋转，得一新扇形A’O’B，其中A点在上，如图(十四)所示，则O点旋转至O’点所经过的轨迹长度为何？

     

    查看答案和解析>>

    科目：初中数学 来源：2010年高级中等学校招生全国统一考试数学卷（四川眉山） 题型：选择题

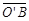    如图(十三)，扇形AOB中，=10， ÐAOB=36°。若固定B点，将此扇形依顺时针方向旋转，得一新扇形A’O’B，其中A点在上，如图(十四)所示，则O点旋转至O’点所经过的轨迹长度为何？

     

    查看答案和解析>>

    同步练习册答案