
【题目】已知:OA⊥OC,∠AOB:∠AOC=2:3,画出图形,并求∠BOC的度数.
【答案】解:∵OA⊥OC, ∴∠AOC=90°,
∵∠AOB:∠AOC=2:3,
∴∠AOB=60°.
因为∠AOB的位置有两种:一种是在∠AOC内,一种是在∠AOC外.
①当在∠AOC内时,∠BOC=90°﹣60°=30°;
②当在∠AOC外时,∠BOC=90°+60°=150°.
综上所述,∠BOC的度数为30°或150°.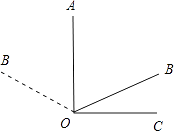
【解析】根据垂直关系知∠AOC=90°,由∠AOB:∠AOC=2:3,可求∠AOB,根据∠AOB与∠AOC的位置关系,分类求解.
【考点精析】通过灵活运用角的运算和垂线的性质,掌握角之间可以进行加减运算;一个角可以用其他角的和或差来表示;垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短即可以解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某汽车销售公司2013年盈利1500万元,2015年盈利2160万元,且从2013年到2015年,每年盈利的年增长率相同.设每年盈利的年增长率为x,根据题意,所列方程正确的是( )
A.1500(1+x)+1500(1+x)2=2160
B.1500x+1500x2=2160
C.1500x2=2160
D.1500(1+x)2=2160
查看答案和解析>>
科目:初中数学 来源: 题型:
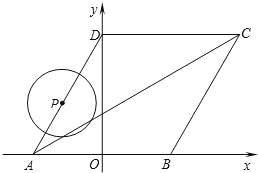
【题目】如图所示,菱形ABCD的顶点A、B在x轴上,点A在点B的左侧,点D在y轴的正半轴上,∠BAD=60°,点A的坐标为(﹣2,0).
(1)求C点的坐标;
(2)求直线AC的函数关系式;
(3)动点P从点A出发,以每秒1个单位长度的速度,按照A→D→C→B→A的顺序在菱形的边上匀速运动一周,设运动时间为t秒.求t为何值时,以点P为圆心、以1为半径的圆与对角线AC相切?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=x2+2y2﹣z,B=﹣4x2+3y2+2z,且A+B+C=0,则多项式C为( )
A. 5x2﹣y2﹣z B. x2﹣y2﹣z C. 3x2﹣y2﹣3z D. 3x2﹣5y2﹣z
查看答案和解析>>
科目:初中数学 来源: 题型:
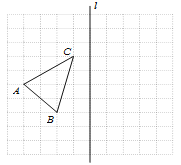
【题目】如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1;(要求:A与A1,B与B1,C与C1相对应)
(2)在(1)问的结果下,连接BB1,CC1,求四边形BB1C1C的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,C为直线l上的一点,A、B为直线l外的两点,过A、B两点分别作直线l的垂线,垂足分别为点D、E,连接BC、AB,AB交直线l于点F,AC=BC,AD=CE.
求证:(1)CE=BE+DE;
(2)AC⊥BC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(14分)探究与发现:如图①,在Rt△ABC中,∠BAC=90°,AB=AC,点D在底边BC上,AE=AD,连结DE.
(1)当∠BAD=60°时,求∠CDE的度数;
(2)当点D在BC (点B、C除外) 上运动时,试猜想并探究∠BAD与∠CDE的数量关系;
(3)深入探究:若∠BAC≠90°,试就图②探究∠BAD与∠CDE的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com