
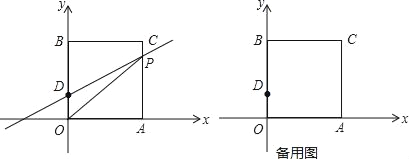
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�O������ԭ�㣬������OACB�Ķ���A��B�ֱ���x��y���ϣ���֪OA��3����DΪy����һ�㣬������Ϊ��0��1����CD��5����P�ӵ�A������ÿ��1����λ���ٶ����߶�A��C��B�ķ����˶�������P���B�غ�ʱֹͣ�˶����˶�ʱ��Ϊt��
��1����B��C�������ꣻ
��2��������OPD�����S����t�ĺ�����ϵʽ��
�ڵ���D����OP�ĶԳƵ�E����x����ʱ�����E�����ꣻ
��3���ڣ�2��������£�ֱ��OP����һ��F��ʹFE+FA��С��
���𰸡���1��B��0��5����C��3��5������2����S����![]() ����E��1��0������3��AD�ij��Ⱦ���AF+EF����Сֵ�����F��Ϊ����
����E��1��0������3��AD�ij��Ⱦ���AF+EF����Сֵ�����F��Ϊ����
��������
��1�����ı���OACB�Ǿ��Σ��õ�BC��OA��3����Rt��BCD�У��ɹ��ɶ����õ�BD��![]() ��4��OB��5���Ӷ���õ�����ꣻ
��4��OB��5���Ӷ���õ�����ꣻ
��2���ٵ���P��AC��ʱ��OD��1��BC��3��S��![]() ��������BC��ʱ��OD��1��BP��5+3��t��8��t���õ�S��
��������BC��ʱ��OD��1��BP��5+3��t��8��t���õ�S��![]() ��1����8��t������
��1����8��t������![]() t+4��
t+4��
�ڵ���D����OP�ĶԳƵ�����x����ʱ���õ���D�ĶԳƵ��ǣ�1��0�������E��1��0����
��3���ɵ�D��E����OP�Գƣ�����AD��OP��F���ҵ���F���Ӷ�ȷ��AD�ij��Ⱦ���AF+EF����Сֵ����Rt��AOD�У��ɹ��ɶ������AD��![]() ����AF+EF����Сֵ��
����AF+EF����Сֵ��![]() ��
��
�⣺��1�����ı���OACB�Ǿ��Σ�
��BC��OA��3��
��Rt��BCD����CD��5��BC��3��
��BD��![]() ��4��
��4��
��OB��5��
��B��0��5����C��3��5����
��2���ٵ���P��AC��ʱ��OD��1��BC��3��
��S��![]() ��
��
������BC��ʱ��OD��1��BP��5+3��t��8��t��
��S��![]() ��1����8��t������
��1����8��t������![]() t+4����t��0��
t+4����t��0��
�ڵ���D����OP�ĶԳƵ�����x����ʱ����D�ĶԳƵ��ǣ�1��0����
��E��1��0����
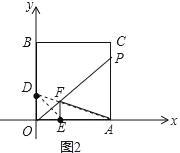
��3����ͼ2�ߵ�D��E����OP�Գƣ�����AD��OP��F��
��AD�ij��Ⱦ���AF+EF����Сֵ�����F��Ϊ����

�ʴ�Ϊ����1��B��0��5����C��3��5������2����S����![]() ����E��1��0������3��AD�ij��Ⱦ���AF+EF����Сֵ�����F��Ϊ����
����E��1��0������3��AD�ij��Ⱦ���AF+EF����Сֵ�����F��Ϊ����


 �ʰ�Ӣ��ͬ����ϰ��ϵ�д�
�ʰ�Ӣ��ͬ����ϰ��ϵ�д� ѧϰʵ����ϵ�д�
ѧϰʵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ1����һ���Ϊ12m����Ϊ20m�ľ��ε���������ͬ�����ĵ�·�����µIJ������ϲ�ƺ��Ҫʹ��ƺ�����Ϊ180m2�����·�Ŀ���
��2�����ڶԸþ���������и��죬��ͼ2���������뽨һ������εı���ƽ�е������ι���ͤ������ͤ���ı�������������εı���ƽ�е��ҿ�����ȵĵ�·����֪��·�Ŀ�Ϊ�����α߳���![]() ������·�����ͤ�����֮���Ǿ��������
������·�����ͤ�����֮���Ǿ��������![]() �����·�Ŀ���
�����·�Ŀ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��O��ֱ��AB����CD���ഹֱ������Ϊ��E. ��O������BF����AD���ӳ����ཻ�ڵ�F����AD=3��cos��BCD=![]() .
.
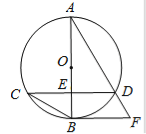
��1����֤��CD��BF��
��2������O�İ뾶��
��3������CD�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���������п���Ŀ��Ϊ�ز���Ŀ��ѡ����Ŀ���ز���ĿΪ��������������Զ��ѡ����ĿΪ50�ס�ʵ�����������������ѡһ�
��1��ÿλ�������� ��ѡ����
��2���û���״ͼ���б��ķ�����Сӱ��С����ѡ��ͬ�ַ����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABCD�У�AB��5��AE��BC���ϵĸߣ�AE��4����Խ���BD�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼΪ���κ���y=ax2+bx+c��a��0����ͼ��������˵������a��0 ��2a+b=0 ��a+b+c��0 �ܵ���1��x��3ʱ��y��0��������ȷ�ĸ���Ϊ��������

A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABC�У� D��E��F����ֱ���AB��AC��BC�ϣ�����D��ֱ�����߶�EF�Ľ���Ϊ��M����֪2��1����2=150�㣬2�� 2����1=30��.
��1����֤��DM��AC��
��2����DE��BC����C =50�㣬���3�Ķ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=ax2+bx+c�ϲ��ֵ�ĺ�����x��������y�Ķ�Ӧֵ���±���

����������x���һ������Ϊ��3��0�����ں���y=ax2+bx+c�����ֵΪ6���������ߵĶԳ�����ֱ��![]() �����ڶԳ�����࣬y��x����������ϱ���֪������˵������ȷ����____________������д��ţ�
�����ڶԳ�����࣬y��x����������ϱ���֪������˵������ȷ����____________������д��ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
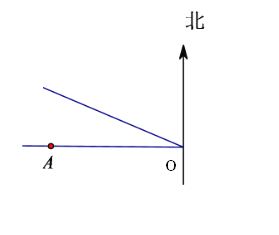
����Ŀ��ij̨������λ��O�㣬̨��������![]()
![]() ���ٶ���ƫ��
���ٶ���ƫ��![]() �����ƶ����ڰ뾶
�����ƶ����ڰ뾶![]() �ķ�Χ�ڽ���Ӱ�죬����A��O������������O�����
�ķ�Χ�ڽ���Ӱ�죬����A��O������������O�����![]() �������ʣ�
�������ʣ�
��1��![]() ���Ƿ���ܴ�̨��Ӱ�죬��˵�����ɣ�
���Ƿ���ܴ�̨��Ӱ�죬��˵�����ɣ�
��2������Ӱ�죬����Ӱ���ʱ���ж��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com