练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图所示，已知，为反比例函数图像上的两点，动点在正半轴上运动，当线段与线段之差达到最大时，点的坐标是
    [     ]
    A.                         
    B.     
    C.                         
    D.
    D
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    精英家教网在八年级上册我们已经知道三角形的中位线具有如下性质：
    三角形的中位线平行于第三边，并且等于它的一半．
    如图所示，已知△ABC和下列四种说法：
    ①D是AB中点；②E是AC中点；③DE=
    12
    BC；④DE∥BC．
    请你以其中的两种说法为条件（①和②不能同时作为条件），其余两种说法为结论，构造一个命题；并判定你所构造的命题是否正确．如果正确请说明理由；如果不正确，请举出反例．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知：在△ABC中，∠ACB=90°，AC=BC，现将一块边长足够大的直角三角板的直角顶点置于AB的中点O处，两直角边分别经过点B、C，然后将三角板绕点O按顺时针方向旋转一个角度反（0°＜a＜90°），旋转后，直角三角板的直角边分别与AC、BC相交于点K、H，四边形CHOK是旋转过程中三角板与△ABC的重叠部分（如图1所示）．那么，在上述旋转过程中：
    （1）如图1，线段BH与CK具有怎样的数量关系？四边形CHOK的面积是否发生变化？请说明你发现的结论的理由．
    （2）如图2，连接HK，
    ①若AK=12，BH=5，求△OKH的面积；
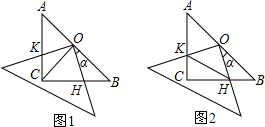
    ②若AC=BC=4，设BH=x，当△CKH的面积为2时，求x的值，并说出此时四边形CHOK是什么特殊四边形．精英家教网

    查看答案和解析>>

    科目：初中数学 来源：同步轻松练习　九年级　数学　上 题型：047

    如图所示，已知正方形ABCD和正方形EFFG有一个公共点A，点G，E不在线段AD，AB上．

    (1)如图，连接DF，BF，若将正方形AEFG绕点A按顺时针方向旋转，判断命题：“在旋转的过程中，线段DF与线段BF的长始终相等”是否正确，若正确请证明；若不正确，请举反例说明．

    (2)若将正方形AEFG绕点A按顺时针方向旋转，连接DG，在旋转的过程中，你能否找到一条线段的长与线段DG的长始终相等，并以图②为例说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

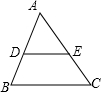    在八年级上册我们已经知道三角形的中位线具有如下性质：
    三角形的中位线平行于第三边，并且等于它的一半．
    如图所示，已知△ABC和下列四种说法：
    ①D是AB中点；②E是AC中点；③DE=数学公式BC；④DE∥BC．
    请你以其中的两种说法为条件（①和②不能同时作为条件），其余两种说法为结论，构造一个命题；并判定你所构造的命题是否正确．如果正确请说明理由；如果不正确，请举出反例．

    查看答案和解析>>

    科目：初中数学 来源：福建省中考真题 题型：解答题

    已知：如图所示，⊙O 是△ABC的外接圆，AB 为⊙O的直径，弦CD 交AB 于E，∠BCD＝∠BAC。
    （1）求证：AC ＝AD；
    （2）过点C作直线CF，交AB的延长线于点F，若∠BCF＝30°， 则结论“CF 一定是⊙O的切线”是否正确？若正确，请证明；若不正确，请举反例。

    查看答案和解析>>

    同步练习册答案