练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知点在的直径延长线上，点为上，过作，与的延长线相交于，为的切线，，．

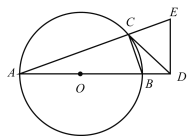
    （1）求证：；

    （2）求的长；

    （3）若的平分线与交于点，为的内心，求的长．

    【答案】（1）见解析；（2）；（3）

    【解析】

    （1）利用同角的余角相等得出∠E=∠ECD，从而得出结论；

    （2）利用直角△OCD和直角△ADE中的勾股定理列出方程解得BD的长；

    （3）连接，，，根据平分求出，利用同弧所对的圆周角相等得出，从而得出，即FP=FB.

    解：（1）证明：连接，

    ∵是的切线，

    ∴，

    ∴，

    ∵，

    ∴，

    ∵，

    ∴，

    ∴，

    ∴．

    （2）∵，

    ∴，

    ∵，

    ∴由勾股定理可得，，

    ∵，

    ∴由勾股定理可得，，

    ∵，

    ∴，

    ∴或（舍去）．

    （3）连接，，，

    ∵平分，

    ∴，

    ∴，

    ∵为直径，，

    ∴，

    ∵为的内心，

    ∴，，

    ∵，

    ∴，

    ∴，

    ∴，

    ∴．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，点A（1，0），已知抛物线y＝﹣x2+mx﹣2m（m是常数），顶点为P．

    （1）当抛物线经过点A时，求顶点P坐标；

    （2）等腰Rt△AOB，点B在第四象限，且OA＝OB．当抛物线与线段OB有且仅有两个公共点时，求m满足的条件；

    （3）无论m取何值，该抛物线都经过定点H．当∠AHP＝45°，求此抛物线解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点C将线段AB分成两部分，若AC2＝BCAB(AC＞BC)，则称点C为线段AB的黄金分割点.某数学兴趣小组在进行抛物线课题研究时，由黄金分割点联想到“黄金抛物线”，类似地给出“黄金抛物线”的定义：若抛物线y＝ax2+bx+c，满足b2＝ac(b≠0)，则称此抛物线为黄金抛物线.

    (Ⅰ)若某黄金抛物线的对称轴是直线x＝2，且与y轴交于点(0，8)，求y的最小值；

    (Ⅱ)若黄金抛物线y＝ax2+bx+c(a＞0)的顶点P为(1，3)，把它向下平移后与x轴交于A(+3，0)，B(x0，0)，判断原点是否是线段AB的黄金分割点，并说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是抛物线的部分图象，其顶点为，与轴交于点，与轴的一个交点为，连接.以下结论：①；②抛物线经过点；③；④当时， .其中正确的是（ ）

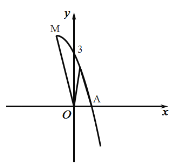
    A.①③B.②③C.①④D.②④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，平移一条抛物线，如果平移后的新抛物线经过原抛物线顶点，且新抛物线的对称轴是y轴，那么新抛物线称为原抛物线的“影子抛物线”．

    （1）已知原抛物线表达式是，求它的“影子抛物线”的表达式；

    （2）已知原抛物线经过点（1，0），且它的“影子抛物线”的表达式是，求原抛物线的表达式；

    （3）小明研究后提出：“如果两条不重合的抛物线交y轴于同一点，且它们有相同的“影子抛物线”，那么这两条抛物线的顶点一定关于y轴对称．”你认为这个结论成立吗？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】4月23日，为迎接“世界读书日”，某书城开展购书有奖活动.顾客每购书满100元获得一次摸奖机会，规则为：一个不透明的袋子中装有4个小球，小球上分别标有数字1，2，3，4，它们除所标数字外完全相同，摇匀后同时从中随机摸出两个小球，则两球所标数字之和与奖励的购书券金额的对应关系如下：

    两球所标数字之和

    3

    4

    5

    6

    7

    奖励的购书券金额（元）

    0

    0

    30

    60

    90

    （1）通过列表或画树状图的方法计算摸奖一次获得90元购书券的概率；

    （2）书城规定：如果顾客不愿意参加摸奖，那么可以直接获得30元的购书券.在“参加摸奖”和“直接获得购书券”两种方式中，你认为哪种方式对顾客更合算？请通过求平均教的方法说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

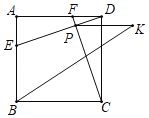
    【题目】如图，正方形ABCD中，AB＝4，E，F分别是边AB，AD上的动点，AE＝DF，连接DE，CF交于点P，过点P作PK∥BC，且PK＝2，若∠CBK的度数最大时，则BK长为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，O是矩形ABCD的对角线的交点，E，F，G，H分别是OA，OB，OC，OD上的点，且AE＝BF＝CG＝DH.

    (1)求证：四边形EFGH是矩形；

    (2)若E，F，G，H分别是OA，OB，OC，OD的中点，且DG⊥AC，OF＝2cm，求矩形ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD中，P是边AD上的一动点，连接BP、CP，过点B作射线交线段CP的延长线于点E，交AD边于点M，且使得∠ABE=∠CBP，如果AB=2，BC=5，AP=x，PM=y.

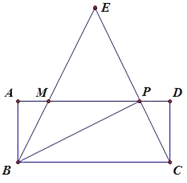
    （1）说明△ABM∽△APB；并求出y关于x的函数关系式，写出自变量x的取值范围；

    （2）当AP=4时，求sin∠EBP的值；

    （3）如果△EBC是以∠EBC为底角的等腰三角形，求AP的长．

    查看答案和解析>>

    同步练习册答案