
【题目】太原市公共自行车的建设速度、单日租骑量等四项指标稳居全国首位.公共自行车车桩的截面示意图如图所示,AB⊥AD,AD⊥DC,点B,C在EF上,EF∥HG,EH⊥HG,AB=75cm,AD=24cm,BC=25cm,EH=4cm,则点A到地面的距离是 cm.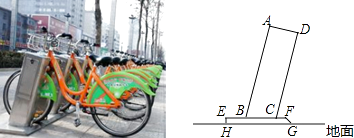
【答案】76
【解析】解:过点A作AM⊥BF于点M,过点C作CN⊥AB于点N,如图所示:
∵AD=24cm,则NC=24cm,
∴BN= ![]() =
= ![]() =7(cm),
=7(cm),
∵∠AMB=∠CNB=90°,∠ABM=∠CBN,
∴△BNC∽△BMA,
∴ ![]() ,
,
∴ ![]() ,
,
解得:AM=72,
故点A到地面的距离=72+4=76(cm).
所以答案是:76.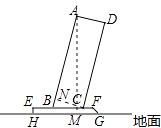
【考点精析】关于本题考查的相似三角形的性质和相似三角形的应用,需要了解对应角相等,对应边成比例的两个三角形叫做相似三角形;测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,直线PM切⊙O于点M,直线PO交⊙O于A、B两点,弦AC∥PM,连接OM、BC.求证: 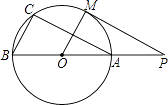
(1)△ABC∽△POM;
(2)2OA2=OPBC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程k2x2﹣2(k+1)x+1=0有两个实数根.
(1)求k的取值范围;
(2)当k=1时,设所给方程的两个根分别为x1和x2 , 求 ![]() +
+ ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在![]() 处,
处,![]() 交AD于点E.
交AD于点E.
(1)试判断△BDE的形状,并说明理由;
(2)若![]() ,
,![]() ,求△BDE的面积.
,求△BDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升8微克(1000微克=1毫克),接着逐步衰减,10小时时血液中含药量为每毫升4微克,每毫升血液中含药量y(微克),随时间x(小时)的变化如图所示.当成人按规定剂量服药后:
(1)求y与x之间的解析式;
(2)如果每毫升血液中含药量不低于3微克或3微克以上时,在治疗疾病时是有效的,那么这个有效时间是多少小时?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在平面直角坐标系中,每个小正方形的边长为1,△ABC的顶点都在格点上,点A的坐标为(-3,2).请按要求分别完成下列各小题:
(1)把△ABC向下平移7个单位,再向右平移7个单位,得到△A1B1C1,画出△A1B1C1;
(2)画出△A1B1C1关于x轴对称的△A2B2C2;
画出△A1B1C1关于y轴对称的△A3B3C3;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知:如图①,点E在正方形ABCD的BC边上,BF⊥AE于点F,DG⊥AE于点G.可知△ADG≌△BAF.(不要求证明)

拓展:如图②,点B、C在∠MAN的边AM、AN上,点E, F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF.
应用:如图③,在等腰三角形ABC中,AB=AC,AB>BC.点D在边B上.CD=2BD.点E, F在线段AD上.∠1=∠2=∠BAC.若△ABC的面积为9,则△ABE与△CDF的面积之和为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学毕业生响应国家“自主创业”的号召,投资开办了一个装饰品商店,该店购进一种新上市的饰品进行了30天的试销售,购进价格为40元/件.销售结束后,得知日销售量P(件)与销售时间x(天)之间有如下关系:P=﹣2x+120(1≤x≤30,且x为整数);销售价格Q(元/件)与销售时间x(天)之间有如下关系:Q= ![]() x+50(1≤x≤30,且x为整数).
x+50(1≤x≤30,且x为整数).
(1)试求出该商店日销售利润w(元)与销售时间x(天)之间的函数关系式;
(2)在这30天的试销售中,哪一天的日销售利润最大,哪一天的日销售利润最小?并分别求出这个最大利润和最小利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O是以AB为直径的△ABC的外接圆,OD∥BC,交⊙O于点D,交AC于点E,连接BD,BD交AC于点F,延长AC到点P,连接PB. 
(1)若PF=PB,求证:PB是⊙O的切线;
(2)如果AB=10,BC=6,求CE的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com