Question

18．已知，△ABC中，AC=BC，∠ACB=90°，CD为中线，点E在射线CA上，作DF⊥DE交直线BC于点F，且AE=3cm，EF=5cm，则AC的长为1cm或7cm．

Answer 1

分析 如图1由等腰三角形三线合一的性质可知CD⊥AB，由直角三角形斜边上中线的性质可知AD=CD，从而可知△ADC为等腰直角三角形，故此可得到∠FCD=∠EAD=135°，根据同角的余角相等可证明∠ADE=∠FDC，从而可证明△EAD≌△FCD，于是得到AE=CF=3，Rt△ECF中，由勾股定理可求得EC=4，于是得到AC=1cm；同理在图2中可求得AC=7cm．

解答 解：如图1所示：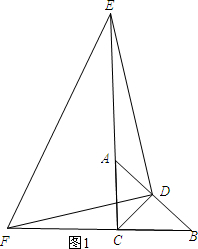

∵AC=CB，CD是中线，
∴CD⊥AB．
∴∠ADF+∠FDC=90°．
∵DE⊥DF，
∴∠EDA+∠ADF=90°．
∴∠ADE=∠FDC．
∵∠ACB=90°，CD是中线，
∴AD=CD．
∵CD⊥AB，AD=CD，
∴∠CAD=∠ACD=45°．
∴∠FCD=∠EAD=135°．
在△EAD和△FCD中$\left\{\begin{array}{l}{∠FCD=∠EAD}\\{AD=CD}\\{∠CAD=∠ACD}\end{array}\right.$
∴△EAD≌△FCD．
∴AE=CF=3．
在Rt△ECF中，EC=$\sqrt{E{F}^{2}-F{C}^{2}}$=4．
∴AC=EC-AE=4-3=1cm．
如图2所示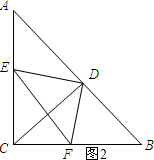

∵AC=CB，CD是中线，
∴CD⊥AB．
∴∠ADF+∠FDC=90°．
∵DE⊥DF，
∴∠EDA+∠ADF=90°．
∴∠ADE=∠FDC．
∵∠ACB=90°，CD是中线，
∴AD=CD．
∵CD⊥AB，AD=CD，
∴∠CAD=∠ACD=45°．
∴∠EAD=∠FCD=45°．
在△EAD和△FCD中$\left\{\begin{array}{l}{∠FCD=∠EAD}\\{AD=CD}\\{∠CAD=∠ACD}\end{array}\right.$
∴△EAD≌△FCD．
∴AE=CF=3．
在Rt△ECF中，EC=$\sqrt{E{F}^{2}-F{C}^{2}}$=4．
∴AC=EC+AE=4+3=7cm．
故答案为：1cm或7cm．

点评 本题主要考查的是等腰三角形的性质、直角三角形斜边上中线的性质、全等三角形的性质和判定、勾股定理的应用，证得△EAD≌△FCD是解题的关键．