

���� ��1�����ɹ���P��m��0����m��0����x��Ĵ��ߣ��ֱ�������y=x2-3x��y=x2-4x�ڵ�N��M���ɱ�ʾ����M��N�����꣬�̶�����߶�MN�ij��ȣ�
���������OP=m��PM=|m2-4m|��PN=|m2-3m|��MN=m��Ȼ��ֱ�ӵ�0��m��3ʱ�뵱m��3ʱȥ������⼴����ô𰸣�
��2���������K��2��-4����Q��$\frac{3}{2}$��$-\frac{9}{4}$�����������ֱ��ֱ��KQ�ĺ�����ϵΪ$y=-\frac{7}{2}x+3$����T��$\frac{6}{7}$��0�����٣����裩��TMN���OKPȫ�ȣ��ֱ�Ӣ�����һ��OP��MN�Ƕ�Ӧ�ߣ������ζ���OK��MN�Ƕ�Ӧ�ߣ�����������KP��MN�Ƕ�Ӧ�ߣ�ȥ������⼴����ô𰸣�
��� �⣺��1���١߹���P��m��0����m��0����x��Ĵ��ߣ��ֱ�������y=x2-3x��y=x2-4x�ڵ�N��M��
���M��m��m2-4m������N��m��m2-3m����
��MN=��m2-3m��-��m2-4m��=m��
�ڸ�������ã�OP=m��PM=|m2-4m|��PN=|m2-3m|��MN=m��
��0��m��3ʱ����PM=m����4m-m2=m����m=3��m=0����ȥ����
��PN=m���� 3m-m2=m����m=2��m=0����ȥ����
��m��3ʱ����PM=m����m2-4m=m����m=5��m=0����ȥ����
�� PN=m ��m2-3m=m����m=4��m=0����ȥ��
���ϣ�m=2��3��4��5��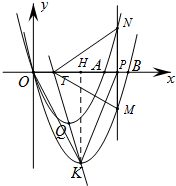
��2��������֪��K��2��-4����Q��$\frac{3}{2}$��$-\frac{9}{4}$����
��ֱ��KQ�ĺ�����ϵΪ$y=-\frac{7}{2}x+3$����T��$\frac{6}{7}$��0����
��������裩��TMN���OKPȫ�ȣ�
��MN=m��OP=m����OP=MN��
������һ��OP��MN�Ƕ�Ӧ�ߣ���KH��x�ᣬ����ΪH�㣬
��TP=KH����TP=m-$\frac{6}{7}$��KH=4��
��$m=4\frac{6}{7}$������3��m��4�ķ�Χ�ڣ�����ȥ��
�����ζ���OK��MN�Ƕ�Ӧ�ߣ�
��OK=$2\sqrt{5}$��
��MN=m=OK=$2\sqrt{5}$������3��m��4�ķ�Χ�ڣ�����ȥ��
����������KP��MN�Ƕ�Ӧ�ߣ�
��$\sqrt{{{��m-2��}^2}+{4^2}}$=m����� m=5��
����3��m��4�ķ�Χ�ڣ�����ȥ��
����費��������TMN���OKP��ȫ�ȣ�
���� �������ڶ��κ������ۺ��⣬�����˶��κ���ͼ���ϵ�����ꡢ�ȱ������ε����ʡ�ȫ�������ε��ж��������Լ�����ϵ���������ʽ��ע�����շ�������˼���Ӧ�ã�ע�֤ⷴ����Ӧ�ã�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m��1 | B�� | m��1 | C�� | m��1 | D�� | m=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2��5 | B�� | -6����-2�� | C�� | 0����-1�� | D�� | 5����-3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
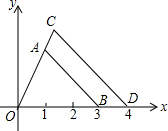 ��֪A��1��2����B��3��0��������AOB������ԭ��OΪλ����������OCD����ͼ����D��4��0�������C������Ϊ��$\frac{4}{3}$��$\frac{8}{3}$����
��֪A��1��2����B��3��0��������AOB������ԭ��OΪλ����������OCD����ͼ����D��4��0�������C������Ϊ��$\frac{4}{3}$��$\frac{8}{3}$�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
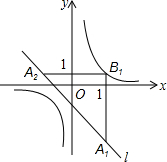 ��ͼ����ƽ��ֱ������ϵxOy�У���ֱ֪��l��y=-x-1��˫����y=$\frac{1}{x}$����l��ȡһ��A1����A1��x��Ĵ��߽�˫�������B1����B1��y��Ĵ��߽�l�ڵ�A2�������������̽������A2��x��Ĵ��߽�˫�����ڵ�B2����B2��y��Ĵ��߽�l�ڵ�A3�������������εõ�l�ϵĵ�A1��A2��A3������An�����ǵ�An�ĺ�����Ϊan����a1=2����a2013=-$\frac{1}{3}$��
��ͼ����ƽ��ֱ������ϵxOy�У���ֱ֪��l��y=-x-1��˫����y=$\frac{1}{x}$����l��ȡһ��A1����A1��x��Ĵ��߽�˫�������B1����B1��y��Ĵ��߽�l�ڵ�A2�������������̽������A2��x��Ĵ��߽�˫�����ڵ�B2����B2��y��Ĵ��߽�l�ڵ�A3�������������εõ�l�ϵĵ�A1��A2��A3������An�����ǵ�An�ĺ�����Ϊan����a1=2����a2013=-$\frac{1}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3�� | B�� | 4�� | C�� | 5�� | D�� | 6�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a2+a3=a5 | B�� | 2a-a=2 | C�� | a6��a3=a2 | D�� | ��a2��3=a6 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com