练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．已知G是等腰直角△ABC的重心，若AC=BC=2，则线段CG的长为$\frac{2}{3}\sqrt{2}$．

    分析 根据三角形的重心到顶点的距离等于到对边中点的距离的2倍解答即可．

    解答 解：∵G是等腰直角△ABC的重心，AC=BC=2，
    ∴CG=$\frac{2}{3}×\frac{2}{\sqrt{2}}=\frac{2}{3}\sqrt{2}$，
    故答案为：$\frac{2}{3}\sqrt{2}$

    点评 本题考查了三角形的重心，熟记三角形的重心到顶点的距离等于到对边中点的距离的2倍是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    19．在△ABC中，AB=AC=5，BC=8，AD⊥BC，垂足为D，BE是△ABC 的中线，AD与BE相交于点G，那么AG的长为2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图，在△ABC中，AC=4，D为BC上一点，CD=2，且△ADC与△ABD的面积比为1：3；
    （1）求证：△ADC∽△BAC；
    （2）当AB=8时，求sinB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．已知：如图，第一象限内的点A，B在反比例函数的图象上，点C在y轴上，BC∥x轴，点A的坐标为（2，4），且cot∠ACB=$\frac{2}{3}$
    求：（1）反比例函数的解析式；
    （2）点C的坐标；
    （3）∠ABC的余弦值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．已知一个坡的坡比为i，坡角为α，则下列等式成立的是（　　）
    A．i=sinαB．i=cosαC．i=tanαD．i=cotα

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

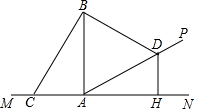    14．如图，在坡AP的坡脚A处竖有一根电线杆AB，为固定电线杆在地面C处和坡面D处各装一根等长的引拉线BC和BD，过点D作地面MN的垂线DH，H为垂足，已知点C、A、H在一直线上，若测得AC=7米，AD=12米，坡角为30°，试求电线杆AB的高度；（精确到0.1米）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．先化简，再求值：（a-$\frac{2a}{a+1}$）÷（$\frac{{{a^2}-2a+1}}{{{a^2}-1}}$），其中a满足a2-3a+2=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

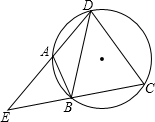    18．如图，点A、B、C、D在同一个圆上，DB=DC，DA、CB的延长线相交于点E，若∠BDC=a，则∠EAB=90°-$\frac{1}{2}$α（用含a的式子表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．数轴上到原点的距离是$\sqrt{3}$的点表示的数是（　　）
    A．$-\sqrt{3}$B．$\sqrt{3}$C．±$\sqrt{3}$D．$\frac{\sqrt{3}}{3}$

    查看答案和解析>>

    同步练习册答案