
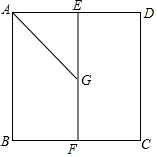
 在边长为1的正方形ABCD中,点E,F分别是边AD,BC的中点,动点G在线段EF上运动,将线段AG绕点G顺时针旋转60°得到线段HG.
在边长为1的正方形ABCD中,点E,F分别是边AD,BC的中点,动点G在线段EF上运动,将线段AG绕点G顺时针旋转60°得到线段HG.分析 (1)根据点H与D不重合,分两种情况:当EG<$\frac{1}{2}\sqrt{3}$时,点H在直线AD的上方;当$\frac{1}{2}\sqrt{3}$<EG≤1时,点H在直线AD的下方,分别根据等腰三角形的性质以及三角形内角和定理,求得∠HDA的度数;
(2)当点G与点E重合时,点H在AD上方,连接AH,求得HD的最大长度$\frac{1}{2}\sqrt{3}$;当点G与点F重合时,H在AD下方时,过H作HM⊥AD于M,根据勾股定理求得DH的最大长度1-$\frac{1}{2}\sqrt{3}$,最后得出点H运动路径长=$\frac{1}{2}\sqrt{3}$+1-$\frac{1}{2}\sqrt{3}$=1.
解答 解:(1)如图所示,当点H与点D重合时,AG=GH=AD=1,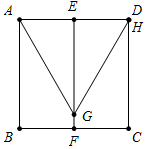
∴EG=$\sqrt{3}$AE=$\frac{1}{2}\sqrt{3}$,
当点H与D不重合时,分两种情况:
①如图所示,当EG<$\frac{1}{2}\sqrt{3}$时,点H在直线AD的上方,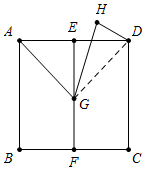
连接GD,设∠GDA=α,则∠GAD=∠GDA=α,
∴∠AGD=180°-2α,
∵∠AGH=60°,
∴∠HGD=120°-2α,
∵GD=GH,
∴∠HDG=30°+α,
∴∠HDA=30°,即点H在过点D且与AD的夹角为30°的直线上;
②如图所示,当$\frac{1}{2}\sqrt{3}$<EG≤1时,点H在直线AD的下方,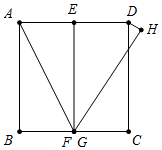
此时,∠HDA=180°-30°=150°;
综上所述,∠HDA的度数为30°或150°;
(2)由(1)可得,当动点G从E运动到F时,点H运动路径为一条线段,
如图所示,当点G与点E重合时,点H在AD上方,连接AH,则△AGH为边长是$\frac{1}{2}$的等边三角形,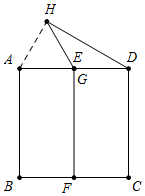
∴∠AHD=90°,
∴HD的最大长度=$\sqrt{3}$AH=$\frac{1}{2}\sqrt{3}$;
如图所示,当点G与点F重合时,H在AD下方时,过H作HM⊥AD于M,则∠HDM=30°,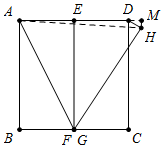
设HM=x,则DH=2x,DM=$\sqrt{3}$x,
在Rt△AHM中,AH=AF=$\sqrt{{1}^{2}+(\frac{1}{2})^{2}}$=$\frac{1}{2}\sqrt{5}$,AM=1+$\sqrt{3}$x,
∵AH2=AM2+HM2,
∴($\frac{1}{2}\sqrt{5}$)2=(1+$\sqrt{3}$x)2+x2,
解得x=$\frac{2-\sqrt{3}}{4}$,
此时DH的最大长度=2x=1-$\frac{1}{2}\sqrt{3}$,
∴点H运动路径长=$\frac{1}{2}\sqrt{3}$+1-$\frac{1}{2}\sqrt{3}$=1.
点评 本题主要考查了旋转的性质,正方形的性质,勾股定理以及等边三角形的性质的综合应用,解决问题的关键是掌握旋转的性质,依据∠HDA=30°得出:当动点G从E运动到F时,点H运动轨迹为一条线段.解题时需要作辅助线构造直角三角形,运用勾股定理进行求解.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
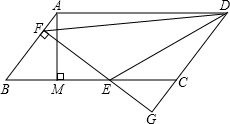 如图,?ABCD中,AB=5,BC=10,BC边上的高AM=4,E为BC边上的一个动点(不与B,C重合),过E作直线AB的垂线,垂足为F,FE与DC的延长线相交于点G,连结DE,DF.
如图,?ABCD中,AB=5,BC=10,BC边上的高AM=4,E为BC边上的一个动点(不与B,C重合),过E作直线AB的垂线,垂足为F,FE与DC的延长线相交于点G,连结DE,DF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
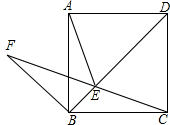 如图所示,在正方形ABCD的对角线BD上取一点E,使得∠BAE=15°,连接AE、CE,延长CE到F,连接BF,使得BC=BF.若AB=1,有下列结论:①AE=EC;②F到BC的距离为$\frac{\sqrt{2}}{2}$;③BE+EC=EF;④S△EBF=$\frac{\sqrt{3}}{12}$.其中正确结论的序号是①③④.
如图所示,在正方形ABCD的对角线BD上取一点E,使得∠BAE=15°,连接AE、CE,延长CE到F,连接BF,使得BC=BF.若AB=1,有下列结论:①AE=EC;②F到BC的距离为$\frac{\sqrt{2}}{2}$;③BE+EC=EF;④S△EBF=$\frac{\sqrt{3}}{12}$.其中正确结论的序号是①③④.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
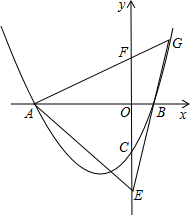 已知抛物线y=$\frac{1}{2}{x}^{2}+2mx-4m-2$(m≥0)与x轴交于A、B两点,A点在B点的左边.与y轴交于点C.
已知抛物线y=$\frac{1}{2}{x}^{2}+2mx-4m-2$(m≥0)与x轴交于A、B两点,A点在B点的左边.与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
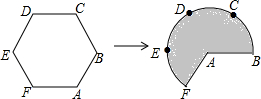 如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为( )
如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为( )| A. | 6π | B. | 18 | C. | 18π | D. | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com